题目内容
点M在圆心为C1的方程x2+y2+6x-2y+1=0上，点N在圆心为C2的方程x2+y2+2x+4y+1=0上，求|MN|的最大值．
考点：圆与圆的位置关系及其判定
专题：直线与圆
分析：由圆C1的方程找出圆心C1的坐标，找出圆心为C2的坐标，然后利用两点间的距离公式即可求出两圆的圆心距，即可得到结论．
解答：
解：由C1的标准方程为（x+3）2+（y-1）2=9，则圆心C1的坐标为（-3，1），半径r=3，
圆C2的标准方程为（x+1）2+（y+2）2=4，则圆心C2的坐标为（-1，-2），半径R=2，
则两圆的圆心距|C1C2|=
=
=
，
则|MN|的最大值为|C1C2|+R+r=
+3+2=5+
．
圆C2的标准方程为（x+1）2+（y+2）2=4，则圆心C2的坐标为（-1，-2），半径R=2，
则两圆的圆心距|C1C2|=
| (-1+3)2+(-1-2)2 |
| 4+9 |
| 13 |
则|MN|的最大值为|C1C2|+R+r=
| 13 |
| 13 |
点评：本题主要考查将圆的一般式方程化为标准式方程，灵活运用两点间的距离公式化简求值，比较基础．
练习册系列答案
相关题目
如图，在正三棱柱ABC-A1B1C1中，点D为棱AB的中点，BC=1，AA1=已知函数f（x）=lnx+
+ax，x∈（0，+∞）（a为实常数）．若f（x）在[2，+∞）上是单调函数，则a的取值范围是（ ）
| 1 |
| x |
A、（-∞，-
| ||
B、（-∞，-
| ||
C、（-∞，0）∪[
| ||
D、（-∞，0）∪（
|
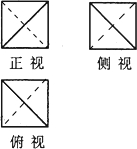正方体的四个顶点构成的几何体的三视图如图，若各视图均为边长为2的正方形，则这个几何体的体积是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，已知AB是半圆O的直径，AB=8，M，N，P是将半圆圆周四等分的三个分点，从A，B，M，N，P这5个点中任取3个点，则这3个点组成直角三角形的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|