题目内容
20．某工厂生产某种产品的产量x（吨）与相应的生产成本y（万元）有如下几组样本数据：| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3.1 | 3.9 | 4.5 |
| A． | 8 | B． | 8.5 | C． | 9 | D． | 9.5 |
分析 计算$\overline{x}$、$\overline{y}$，求出回归系数，写出回归方程，
据此模型预测生产成本是6.7万元时相应的产量约是多少．
解答 解：计算$\overline{x}$=$\frac{1}{4}$×（3+4+5+6）=4.5，
$\overline{y}$=$\frac{1}{4}$×（2.5+3.1+3.9+4.5）=3.5；
代入回归方程$\stackrel{∧}{y}$=0.8x+$\stackrel{∧}{a}$得
3.5=0.8×4.5+$\stackrel{∧}{a}$，
解得$\stackrel{∧}{a}$=-0.1；
∴回归方程为$\stackrel{∧}{y}$=0.8x-0.1，
令$\stackrel{∧}{y}$=0.8x-0.1=6.7，
解得x=8.5，
据此模型预测生产成本是6.7万元时，其相应的产量约是8.5吨．
故选：B．
点评 本题考查了线性回归方程的求法与应用问题，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．下列命题中的真命题是（ ）
| A． | ?x0∈R，使得sinx+cosx=$\frac{3}{2}$ | B． | ?x0∈R，使得$x_0^2-{x_0}+1=0$ | ||
| C． | ?x∈（0，+∞），ex＞x+1 | D． | ?x∈（0，π），sinx＞cosx |
11．抛物线y2=4x上有两点A、B到焦点的距离之和为8，则A、B到y轴的距离之和为（ ）
| A． | 8 | B． | 7 | C． | 6 | D． | 5 |
8．设A（1，1）、B（7，4），点C满足$\overrightarrow{AC}$=2$\overrightarrow{CB}$，则点C的坐标是（ ）
| A． | （3，2） | B． | （3，5） | C． | （5，3） | D． | （8，5） |
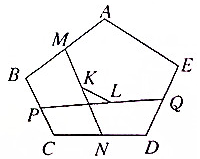如图所示，五边形ABC 中，点M、N、P、Q分别是AB、CD、BC、DE的中点，K和L分别是MN和PQ的中点．求证：$\overrightarrow{KL}$=$\frac{1}{4}$$\overrightarrow{AE}$．