题目内容
2.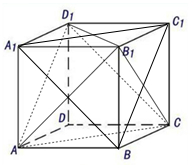 正方体ABCD-A1B1C1D1中,连接A1C1,A1B,BC1,AD1,AC,CD1.
正方体ABCD-A1B1C1D1中,连接A1C1,A1B,BC1,AD1,AC,CD1.(1)求证:A1C1∥平面ACD1;
(2)求证:平面A1BC1∥平面ACD1;
(3)设正方体ABCD-A1B1C1D1的棱长为a,求四面体ACB1D1的体积.
分析 (1)由AA1$\stackrel{∥}{=}$CC1可得四边形A1ACC1是平行四边形,故A1C1∥AC,从而A1C1∥平面ACD1;
(2)同理与(1)的证明可得BC1∥平面ACD1.于是得出平面A1BC1∥平面ACD1;
(3)用正方体的体积减去四个小棱锥的体积即可得出所求几何体的体积.
解答 (1)证明:∵AA1∥CC1,AA1=CC1,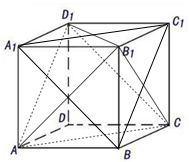
∴四边形A1ACC1是平行四边形,
∴A1C1∥AC.
又AC?平面ACD1,A1C1?平面ACD1,
∴A1C1∥平面ACD1.
(2)证明:∵AB∥C1D1,AB=C1D1,
∴四边形ABC1D1是平行四边形,
∴AD1∥BC1,
又BC1?平面ACD1,AD1?平面ACD1,
∴BC1∥平面ACD1.
又A1C1∥平面ACD1.A1C1?平面A1BC1,BC1?平面A1BC1,A1C1∩BC1=C1,
∴平面A1BC1∥平面A1BC1.
(3)V${\;}_{{A}_{1}-A{B}_{1}{D}_{1}}$=V${\;}_{{B}_{1}-ABC}$=V${\;}_{C-{B}_{1}{C}_{1}{D}_{1}}$=V${\;}_{{D}_{1}-ACD}$=$\frac{1}{3}×\frac{1}{2}×{a}^{2}×a$=$\frac{{a}^{3}}{6}$.
∴四面体ACB1D1的体积V=a3-V${\;}_{{A}_{1}-A{B}_{1}{D}_{1}}$-V${\;}_{{B}_{1}-ABC}$-V${\;}_{C-{B}_{1}{C}_{1}{D}_{1}}$-V${\;}_{{D}_{1}-ACD}$=a3-4V${\;}_{{B}_{1}-ABC}$=a3-$\frac{2}{3}{a}^{3}$=$\frac{{a}^{3}}{3}$.
点评 本题考查了正方体的结构特征,线面平行,面面平行的判定,棱锥的体积计算,基础题.

| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
| A. | a<5 | B. | |a|<4 | C. | a2<25 | D. | -5<a<5 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
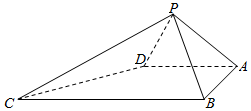 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.