题目内容
7．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-1，x≤0}\\{lo{g}_{2}x，x＞0}\end{array}\right.$，则函数y=f（x）的零点个数是（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 利用分段函数，分别通过解方程求出方程的根，即可求出函数的零点的个数．
解答 解：函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-1，x≤0}\\{lo{g}_{2}x，x＞0}\end{array}\right.$，
则x≤0时，x2-1=0，解得x=-1．
x＞0时，log2x=0，解得x=1．
函数y=f（x）的零点个数是：2．
故选：C．
点评 本题考查函数的零点个数与方程根的关系，考查计算能力．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
2．若函数f（x）=$\frac{a-sinx}{cosx}$在区间（$\frac{π}{6}$，$\frac{π}{3}$）上单调递增，则实数a的取值范围是（ ）
| A． | [2，+∞） | B． | （2，+∞） | C． | [$\sqrt{3}$，+∞） | D． | （-$\sqrt{3}$，+∞） |
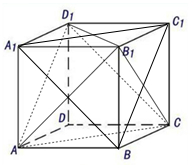正方体ABCD-A1B1C1D1中，连接A1C1，A1B，BC1，AD1，AC，CD1．
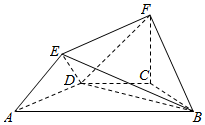如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，若CB=CD=CF=a．
6．设f（x）满足：①任意x∈R，有f（x）+f（2-x）=0；②当x≥1时，f（x）=|x-a|-1，（a＞0），若x∈R，恒有f（x）＞f（x-m），则m的取值范围是（ ）
| A． | （0，+∞） | B． | （4，+∞） | C． | （3，+∞） | D． | （5，+∞） |