题目内容
14.已知复数$z=\frac{10}{3+i}-2i$,其中i是虚数单位,则|z|=( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
分析 根据复数的运算性质求出z,从而求出z的模.
解答 解:∵$z=\frac{10}{3+i}-2i$=3-3i,
∴|z|=$\sqrt{{3}^{2}{+(-3)}^{2}}$=3$\sqrt{2}$,
故选:C.
点评 本题考查了复数的运算,考查复数求模问题,是一道基础题.

练习册系列答案
相关题目
6.设f(x)满足:①任意x∈R,有f(x)+f(2-x)=0;②当x≥1时,f(x)=|x-a|-1,(a>0),若x∈R,恒有f(x)>f(x-m),则m的取值范围是( )
| A. | (0,+∞) | B. | (4,+∞) | C. | (3,+∞) | D. | (5,+∞) |
4.在复平面内,复数$\frac{3-i}{1-i}$对应的点的坐标为( )
| A. | (2,1) | B. | (1,-2) | C. | (1,2) | D. | (2,-1) |
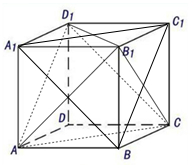 正方体ABCD-A1B1C1D1中,连接A1C1,A1B,BC1,AD1,AC,CD1.
正方体ABCD-A1B1C1D1中,连接A1C1,A1B,BC1,AD1,AC,CD1.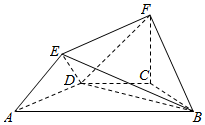 如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,若CB=CD=CF=a.
如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,若CB=CD=CF=a. 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左顶点(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于D,交y轴于E.
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左顶点(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于D,交y轴于E.