题目内容
12．设向量$\overrightarrow a$=（-2，3），$\overrightarrow b$=（-1，x-1），若$\overrightarrow a$∥$\overrightarrow b$，则x=$\frac{5}{2}$．分析 根据平面向量的坐标表示与共线定理，列出方程求出x的值．
解答 解：∵向量$\overrightarrow a$=（-2，3），$\overrightarrow b$=（-1，x-1），且$\overrightarrow a$∥$\overrightarrow b$，
∴-2（x-1）-3×（-1）=0，
解得x=$\frac{5}{2}$．
故答案为：$\frac{5}{2}$．
点评 本题考查了平面向量的坐标表示与共线定理的应用问题，是基础题目．
练习册系列答案
相关题目
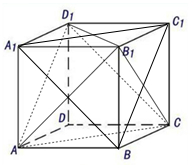正方体ABCD-A1B1C1D1中，连接A1C1，A1B，BC1，AD1，AC，CD1．
如图，在平面直角坐标系xOy中，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，左顶点（-4，0），过点A作斜率为k（k≠0）的直线l交椭圆C于D，交y轴于E．
水是最常见的物质之一，是包括人类在内所有生命生存的重要资源，也是生物体最重要的组成部分．为了推动对水资源进行综合性统筹规划和管理，加强水资源保护，解决日益严峻的淡水缺乏问题，开展广泛的宣传以提高公众对开发和保护水资源的认识．中国水利部确定每年的3月22日至28日为“中国水周”，以提倡市民节约用水．某市统计局调查了该市众多家庭的用水量情况，绘制了月用水量的频率分布直方图，如图所示．将月用水量落入各组的频率视为概率，并假设每天的用水量相互独立．
4．在复平面内，复数$\frac{3-i}{1-i}$对应的点的坐标为（ ）
| A． | （2，1） | B． | （1，-2） | C． | （1，2） | D． | （2，-1） |
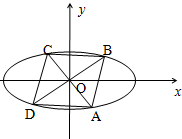已知M（-2$\sqrt{2}$，0），N（2$\sqrt{2}$，0）为椭圆的左、右顶点，P是椭圆上异于M，N的动点，且△PMN的面积最大值为4$\sqrt{2}$．
2．设Sn是等比数列{an}的前n项和，若S2=2，S6=4，则S4=（ ）
| A． | 1+$\sqrt{5}$ | B． | $\frac{10}{3}$ | C． | 2$\sqrt{2}$ | D． | 3 |