题目内容
20.数列{an}的前n项和为Sn,若a1=1,an+1=3Sn(n≥1),则数列{an}的通项公式an=$\left\{\begin{array}{l}{1,n=1}\\{3×{4}^{n-2},n≥2}\end{array}\right.$.分析 先看n≥2根据题设条件可知an=3Sn-1,两式想减整理得an+1=4an,判断出此时数列{an}为等比数列,a2=3a1=3,公比为4,求得n≥2时的通项公式,最后综合可得答案.
解答 解:当n≥2时,an=3Sn-1,
∴an+1-an=3Sn-3Sn-1=3an,
即an+1=4an,
∴数列{an}为等比数列,a2=3a1=3,公比为4
∴an=3•4n-2,
当n=1时,a1=1
∴数列{an}的通项公式${a_n}=\left\{\begin{array}{l}1(n=1)\\ 3×{4^{n-2}}(n≥2)\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{1,n=1}\\{3×{4}^{n-2},n≥2}\end{array}\right.$.
点评 本题主要考查了数列的递推式求数列通项公式.解题的最后一定要验证a1.是基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
10.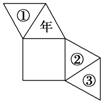 某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )
某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )
 某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )
某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )| A. | 快、新、乐 | B. | 乐、新、快 | C. | 新、乐、快 | D. | 乐、快、新 |
11.已知集合A={x|x-x2≥0},B={x|y=lg(2x-1)},则A∩B=( )
| A. | $[{0,\frac{1}{2}})$ | B. | [0,1] | C. | $({\frac{1}{2},1}]$ | D. | $({\frac{1}{2},+∞})$ |
15.下列是函数y=-(x-3)|x|的递增区间是( )
| A. | (-∞,3) | B. | (0,3) | C. | $({0,\frac{3}{2}})$ | D. | $({\frac{3}{2},3})$ |
5.从集合{1,2,3,4} 中有放回地随机抽取2次,每次抽取1个数,则2次抽取数之和等于4的概率为( )
| A. | $\frac{4}{16}$ | B. | $\frac{3}{16}$ | C. | $\frac{2}{16}$ | D. | $\frac{1}{16}$ |