题目内容
函数f（x）=2sin（ωx+φ）（ω＞0）的图象经过A（-
，-2）、B（
，2）两点，则ω（ ）
| π |
| 6 |
| π |
| 4 |
| A、最大值为3 | ||
| B、最小值为3 | ||
C、最大值为
| ||
D、最小值为
|
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：当A、B为函数的图象的相邻的两个顶点时，函数的周期最小，ω最大，此时，由
×
=
+
，求得ω的值
| 1 |
| 2 |
| 2π |
| ω |
| π |
| 4 |
| π |
| 6 |
解答：
解：由题意可得A、B为函数的图象的顶点，
故当A、B为函数的图象的相邻的两个顶点时，周期最小，ω最大，
此时，
×
=
+
=
，ω=
，
故选：C．
故当A、B为函数的图象的相邻的两个顶点时，周期最小，ω最大，
此时，
| 1 |
| 2 |
| 2π |
| ω |
| π |
| 4 |
| π |
| 6 |
| 5π |
| 12 |
| 12 |
| 5 |
故选：C．
点评：本题主要考查函数y=Asin（ωx+φ）的图象和性质，属于基础题．
练习册系列答案
相关题目
若f（x）=-
x2+blnx在[1，+∞）上是减函数，则b的取值范围是（ ）
| 1 |
| 2 |
| A、[-1，+∞） |
| B、（-1，+∞） |
| C、（-∞，1] |
| D、（-∞，-1） |
过双曲线
-
=1（a＞0，b＞0）的左焦点F（-c，0）（c＞0）作斜率为
的直线交双曲线右支于点P，E为FP的中点，O为坐标原点，且OE⊥FP，则双曲线离心率为 （ ）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
要得到函数y=2cos2x的图象，需要把函数y=sin2x的图象（ ）
A、向右平移
| ||
B、向左平移
| ||
C、向左平移
| ||
D、向右平移
|
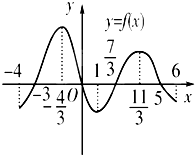已知函数y=f（x）在定义域[-4，6]内可导，其图象如图，记y=f（x）的导函数为y=f′（x），则不等式f′（x）≤0的解集为（ ）A、[-
| ||||
B、[-3，0]∪[
| ||||
C、[-4，-
| ||||
| D、[-4，-3]∪[0，1]∪[5，6] |
已知f′（x）为f（x）的导数，若f′（x）＜f（x）对于任意的x∈R都成立，则（ ）
A、f（0）＜
| ||
B、f（0）＞
| ||
C、f（0）=
| ||
D、
|