题目内容
在直角坐标系xOy中,曲线C1的参数方程为
(α为参数),M为C1上的动点,P点满足
=2
,点P的轨迹为曲线C2.已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线θ=
与C1的异于极点的交点为A,与C2的异于极点的交点为B,
(1)求曲线C1与C2的直角坐标方程;
(2)求线段AB的长.
|
| OP |
| OM |
| π |
| 3 |
(1)求曲线C1与C2的直角坐标方程;
(2)求线段AB的长.
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(1)先设出点P的坐标,然后根据点P满足的条件代入曲线C1的方程即可求出曲线C2的方程;
(2)根据(1)将求出曲线C1的极坐标方程,分别求出射线θ=
与C1的交点A的极径为ρ1,以及射线θ=
与C2的交点B的极径为ρ2,最后根据|AB|=|ρ2-ρ1|求出所求.
(2)根据(1)将求出曲线C1的极坐标方程,分别求出射线θ=
| π |
| 3 |
| π |
| 3 |
解答:
解:(1)设P(x,y),则由条件知道M(
,
),
由于M点在C1上,所以
即
,
从而C2的参数方程为
(α为参数),
所以曲线C1与C2的直角坐标方程分别为x2+(y-2)2=4,x2+(y-4)2=16;
(2)曲线C1的极坐标方程为ρ=4sinθ;曲线C2的极坐标方程为ρ=8sinθ.
射线θ=
与C1的交点A的极径为ρ1=4sin
,
射线θ=
与C2的交点B的极径为ρ2=8sin
.
所以|AB|=|ρ2-ρ1|=2
.
| x |
| 2 |
| y |
| 2 |
由于M点在C1上,所以
|
|
从而C2的参数方程为
|
所以曲线C1与C2的直角坐标方程分别为x2+(y-2)2=4,x2+(y-4)2=16;
(2)曲线C1的极坐标方程为ρ=4sinθ;曲线C2的极坐标方程为ρ=8sinθ.
射线θ=
| π |
| 3 |
| π |
| 3 |
射线θ=
| π |
| 3 |
| π |
| 3 |
所以|AB|=|ρ2-ρ1|=2
| 3 |
点评:本题考查点的极坐标和直角坐标的互化,以及轨迹方程的求解和线段的度量,属于中档题.

练习册系列答案
相关题目
已知双曲线kx2-y2=1(k>0)的一条渐近线与直线2x+y-3=0垂直,则双曲线的离心率是( )
A、
| ||||
B、
| ||||
C、4
| ||||
D、
|
已知正方体ABCD-A1B1C1D1中,E、F分别是A1D1、A1C1的中点,则异面直线AE与CF所成的角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=2sin(ωx+φ)(ω>0)的图象经过A(-
,-2)、B(
,2)两点,则ω( )
| π |
| 6 |
| π |
| 4 |
| A、最大值为3 | ||
| B、最小值为3 | ||
C、最大值为
| ||
D、最小值为
|
已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y=-
x3+49x-234则使该生产厂家获得最大年利润的年产量为( )
| 1 |
| 3 |
| A、13万件 | B、11万件 |
| C、9万件 | D、7万件 |
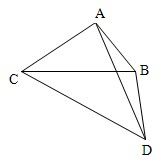 在三棱锥A-BCD中,平面ACB⊥平面BCD.在等腰直角三角形ABC中,AC=AB,AC=6,在Rt△BCD中,BC⊥BD,∠BCD=30°
在三棱锥A-BCD中,平面ACB⊥平面BCD.在等腰直角三角形ABC中,AC=AB,AC=6,在Rt△BCD中,BC⊥BD,∠BCD=30° AB是⊙O的直径,C为圆上一点,AB=2,AC=1,P为⊙O所在平面外一点,且PA⊥⊙O,PB与平面所成角为45°
AB是⊙O的直径,C为圆上一点,AB=2,AC=1,P为⊙O所在平面外一点,且PA⊥⊙O,PB与平面所成角为45°