题目内容
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)(c>0)作斜率为
的直线交双曲线右支于点P,E为FP的中点,O为坐标原点,且OE⊥FP,则双曲线离心率为 ( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,设右焦点为F′,则∠FPF′=90°,由斜率为
的直线交双曲线右支于点P,可得PF′=c,PF=
c.利用双曲线的定义,即可求出双曲线离心率.
| ||
| 3 |
| 3 |
解答:
解:由题意,设右焦点为F′,则
∵E为FP的中点,O为坐标原点,
∴OE∥PF′,
∵OE⊥FP,
∴∠FPF′=90°,
∵斜率为
的直线交双曲线右支于点P,
∴PF′=c,PF=
c,
∴(
-1)c=2a,
∴e=
=
=
+1.
故选:B.
∵E为FP的中点,O为坐标原点,
∴OE∥PF′,
∵OE⊥FP,
∴∠FPF′=90°,
∵斜率为
| ||
| 3 |
∴PF′=c,PF=
| 3 |
∴(
| 3 |
∴e=
| c |
| a |
| 2 | ||
|
| 3 |
故选:B.
点评:本题考查双曲线离心率,考查学生的计算能力,确定PF′=c,PF=
c是关键.
| 3 |

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
已知双曲线kx2-y2=1(k>0)的一条渐近线与直线2x+y-3=0垂直,则双曲线的离心率是( )
A、
| ||||
B、
| ||||
C、4
| ||||
D、
|
已知函数f(x)=ax2009+bsinx+1,且f(m)=2,则f(-m)=( )
| A、0 | B、1 | C、4 | D、-1 |
当输入x=-4时,如图的程序运行的结果是( )


| A、7 | B、8 | C、9 | D、15 |
过双曲线x2-y2=1的右焦点且斜率是1的直线与双曲线的交点个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
已知正方体ABCD-A1B1C1D1中,E、F分别是A1D1、A1C1的中点,则异面直线AE与CF所成的角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=2sin(ωx+φ)(ω>0)的图象经过A(-
,-2)、B(
,2)两点,则ω( )
| π |
| 6 |
| π |
| 4 |
| A、最大值为3 | ||
| B、最小值为3 | ||
C、最大值为
| ||
D、最小值为
|
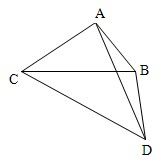 在三棱锥A-BCD中,平面ACB⊥平面BCD.在等腰直角三角形ABC中,AC=AB,AC=6,在Rt△BCD中,BC⊥BD,∠BCD=30°
在三棱锥A-BCD中,平面ACB⊥平面BCD.在等腰直角三角形ABC中,AC=AB,AC=6,在Rt△BCD中,BC⊥BD,∠BCD=30°