Question

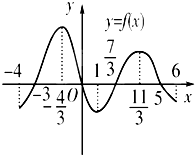已知函数y=f（x）在定义域[-4，6]内可导，其图象如图，记y=f（x）的导函数为y=f′（x），则不等式f′（x）≤0的解集为（　　）

• A、[-

  4

  3

  ，1]∪[

  11

  3

  ，6]
• B、[-3，0]∪[

  7

  3

  ，5]
• C、[-4，-

  4

  3

  ]∪[1，

  7

  3

  ]
• D、[-4，-3]∪[0，1]∪[5，6]

Answer 1

考点：利用导数研究函数的单调性

专题：导数的综合应用

分析：根据函数单调性和导数之间的关系，只要判断函数单调递减的区间即可得到结论．

解答： 解：由函数图象可知，不等式f′（x）≤0的解集，对应函数单调递减的区间，
由图象可知函数的单调递减区间为[-

4

3

，1]∪[

11

3

，6]，
故选：A

点评：本题主要考查函数图象的识别和应用，根据函数单调性和导数之间的关系是解决本题的关键．