题目内容
18.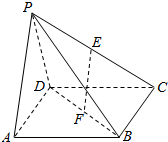 在四棱锥P-ABCD中,底面ABCD是正方形,AP⊥PD,侧面PAD⊥底面ABCD,点E、F分别为PC、BD的中点.
在四棱锥P-ABCD中,底面ABCD是正方形,AP⊥PD,侧面PAD⊥底面ABCD,点E、F分别为PC、BD的中点.求证:(1)平面PDC⊥平面PAD;
(2)EF⊥平面PDC.
分析 (1)由平面PAD⊥平面ABCD,又ABCD是正方形,可证CD⊥AD,CD⊥平面PAD,结合CD?平面PDC,即可证明平面PDC⊥平面PAD.
(2)连接AC,则EF∥PA,要证明EF⊥平面PDC,只需证PA⊥平面PDC即可,已知PA⊥PD,只需再证明PA⊥CD,而这需要证明CD⊥平面PAD,由(1)即可得证.
解答 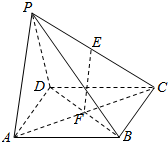 证明:(1)因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
证明:(1)因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
又由于ABCD是正方形,CD⊥AD,
所以CD⊥平面PAD,
因为CD?平面PDC,
∴平面PDC⊥平面PAD(6分)
(2)连接AC,则F是AC的中点,在△CPA中,EF∥PA(9分)
∵由(1)可得CD⊥平面PAD,
∴CD⊥PA(12分)
又PA⊥PD,
而CD∩PD=D,
∴PA⊥平面PDC,
又EF∥PA,所以EF⊥平面PDC(14分)
点评 本题考查线面平行的判定及线面垂直的判定,而其中的转化思想的应用值得注意,将线面平行转化为线线平行;证明线面垂直,转化为线线垂直,在证明线线垂直时,往往还要通过线面垂直来进行.

练习册系列答案
相关题目
8.把复数z的共轭复数记作$\overline z$,i为虚数单位,若z=1+i,则(2+z)•$\overline z$=( )
| A. | 4+2i | B. | 4-2i | C. | 2+4i | D. | 4 |
9.已知M={y∈R|y=x2},N={x∈R|x2+y2=2},则M∩N=( )
| A. | {(-1,1),(1,1)} | B. | {1} | C. | [0,1] | D. | $[{0,\sqrt{2}}]$ |
6.已知抛物线M:y2=4x,圆N:(x-1)2+y2=r2(其中r为常数,r>0).过点(1,0)的直线l交圆N于C、D两点,交抛物线M于A、B两点,且满足|AC|=|BD|的直线l只有三条,则( )
| A. | r∈(0,1] | B. | r∈(1,$\frac{3}{2}$] | C. | r∈($\frac{3}{2}$,2] | D. | r∈(2,+∞) |