题目内容
9.已知M={y∈R|y=x2},N={x∈R|x2+y2=2},则M∩N=( )| A. | {(-1,1),(1,1)} | B. | {1} | C. | [0,1] | D. | $[{0,\sqrt{2}}]$ |
分析 求出M中y的范围确定出M,求出B中x的范围确定出N,找出两集合的交集即可.
解答 解:由M中y=x2≥0,得到M=[0,+∞),
由N中x2+y2=2,得到-$\sqrt{2}$≤x≤$\sqrt{2}$,即N=[-$\sqrt{2}$,$\sqrt{2}$],
则M∩N=[0,$\sqrt{2}$],
故选:D.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
20.命题“所有奇数的立方是奇数”的否定是( )
| A. | 所有奇数的立方不是奇数 | B. | 不存在一个奇数,它的立方是偶数 | ||
| C. | 存在一个奇数,它的立方是偶数 | D. | 不存在一个奇数,它的立方是奇数 |
17.执行如图所示的程序框图,则输出的结果是( )


| A. | 21 | B. | 34 | C. | 55 | D. | 89 |
14.函数y=cos($\frac{π}{4}$-2x)的单调递减区间是( )
| A. | [$\frac{π}{8}$+2kπ,$\frac{5π}{8}$+2kπ](k∈Z) | B. | [$\frac{π}{8}$+kπ,$\frac{5π}{8}$+kπ](k∈Z) | ||
| C. | [-$\frac{3π}{8}$+2kπ,$\frac{π}{8}$+2kπ](k∈Z) | D. | [-$\frac{3π}{8}$+kπ,$\frac{π}{8}$+kπ](k∈Z) |
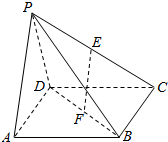 在四棱锥P-ABCD中,底面ABCD是正方形,AP⊥PD,侧面PAD⊥底面ABCD,点E、F分别为PC、BD的中点.
在四棱锥P-ABCD中,底面ABCD是正方形,AP⊥PD,侧面PAD⊥底面ABCD,点E、F分别为PC、BD的中点.