题目内容
7.如图,在等腰直角△ABC中,过直角顶点C作射线CM交AB于M,则使得AM小于AC的概率为$\frac{3}{4}$.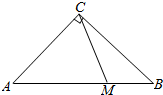
分析 欲求AM的长大于AC的长的概率,先求出M点可能在的位置的长度,利用几何概型的概率公式即可得到结论.
解答 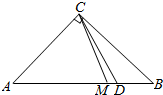 解:在等腰直角三角形ABC中,设AC长为1,则AB长为$\sqrt{2}$,
解:在等腰直角三角形ABC中,设AC长为1,则AB长为$\sqrt{2}$,
在AB上取点D,使AD=1,则若M点在线段AD上,满足条件AM<AC.
则M位于AD上,则|AD|=1,|AB|=$\sqrt{2}$,
则∠ACD=$\frac{18{0}^{0}-4{5}^{0}}{2}$=$\frac{135°}{2}$,
∴AM的长小于AC的长的概率P=$\frac{\frac{135°}{2}}{90°}$=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 本题主要考查几何概型的概率的计算,求出满足条件的M的位置是解决本题的关键.

练习册系列答案
相关题目
17.执行如图所示的程序框图,则输出的结果是( )


| A. | 21 | B. | 34 | C. | 55 | D. | 89 |
15.在圆C:(x-2)2+(y-2)2=8内,过点P(1,1)的最长的弦为AB,最短的弦为DE,则四边形ADBE的面积为( )
| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
2.直线a、b平行于平面α,则a,b的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 异面 | D. | 以上均有可能 |
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),P为双曲线上任一点,若双曲线的离心率的取值范围为[$\sqrt{2}$,2],则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$最小值的取值范围是( )
| A. | [$\frac{1}{2}$,$\frac{3}{4}$] | B. | [-$\frac{3}{4}$,-$\frac{1}{2}$] | C. | [-$\frac{1}{2}$,-$\frac{1}{4}$] | D. | [$\frac{1}{4}$,$\frac{1}{2}$] |
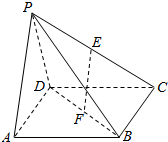 在四棱锥P-ABCD中,底面ABCD是正方形,AP⊥PD,侧面PAD⊥底面ABCD,点E、F分别为PC、BD的中点.
在四棱锥P-ABCD中,底面ABCD是正方形,AP⊥PD,侧面PAD⊥底面ABCD,点E、F分别为PC、BD的中点.