题目内容

8．把复数z的共轭复数记作$\overline z$，i为虚数单位，若z=1+i，则（2+z）•$\overline z$=（　　）
A．4+2iB．4-2iC．2+4iD．4

分析 直接利用复数的乘法运算法则化简求解即可．

解答 解：复数z的共轭复数记作$\overline z$，i为虚数单位，若z=1+i，
则（2+z）•$\overline z$=（3+i）（1-i）=3+i-3i+1=4-2i．
故选：B．

点评 本题考查复数的代数形式混合运算，基本知识的考查．

练习册系列答案
相关题目
18．已知函数f（x）=-x2+ax-b．
（1）若a、b分别表示甲、乙两人各掷一次骰子所得的点数，求f（x）=0有解的概率；
（2）若a、b都是从区间[0，4]任取的一个实数，求f（1）＞0成立的概率．
19．已知抛物线y2=8x的准线过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的一个焦点，且双曲线的实轴长为2，则该双曲线的方程为${x^2}-\frac{y^2}{3}=1$．
16．已知对于圆x2+y2-2y=0上任意一点P，不等式x+y+m≥0恒成立，则实数m的取值范围为（　　）
A．m≥-1B．m≥$\sqrt{2}$-1C．m≤-$\sqrt{2}$-1D．m≥$\sqrt{2}-1或m≤-\sqrt{2}$-1
3．集合A={0，2，a}，B={1，a2}，若A∪B={0，1，2，3，9}，则a的值为（　　）
A．0B．1C．2D．3
13．下列各式中，最小值为2的是（　　）
A．$\frac{x}{y}+\frac{y}{x}$B．$\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$C．5x+5-xD．tanx+cotx
20．命题“所有奇数的立方是奇数”的否定是（　　）
A．所有奇数的立方不是奇数B．不存在一个奇数，它的立方是偶数
C．存在一个奇数，它的立方是偶数D．不存在一个奇数，它的立方是奇数
17．执行如图所示的程序框图，则输出的结果是（　　）
A．21B．34C．55D．89
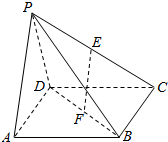18．在四棱锥P-ABCD中，底面ABCD是正方形，AP⊥PD，侧面PAD⊥底面ABCD，点E、F分别为PC、BD的中点．
求证：（1）平面PDC⊥平面PAD；
（2）EF⊥平面PDC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网