题目内容
已知向量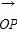
＝(2cosx＋1，cos2x－sinx＋1)，
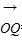＝(cosx，－1)，f(x)＝·.
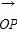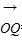(1)求函数f(x)的最小正周期；
(2)当x∈[0，
]时，求函数f(x)的最大值及取得最大值时的x值．
(1)∵＝
(2cosx＋1，cos2x－sinx＋1)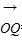，＝(cosx，－1)，
∴f(x)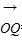＝·＝(2cosx＋1)cosx－(cos2x－sinx＋1)
＝2cos2x＋cosx－cos2x＋sinx－1
＝cosx＋sinx＝
sin(x＋
)，
∴函数f(x)最小正周期T＝2π.
(2)∵x∈[0，]，
∴x＋
∈[，
]，
∴当x＋＝
，
即x＝时，f(x)＝sin(x＋)取到最大值.
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
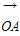＝(3，－4)，
＝(6，－3)，
＝(m，m＋1)，若
∥
B．－
D.
的值为( )
，则
等于( )
则
·
取得最小值时，点B的个数是( )
－(2n－1)an－2n＝0.
，求数列{bn}的前n项和Tn.
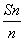)(n∈N*)总在直线y＝
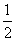x＋
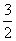上．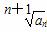
(n∈N*)，试问数列{bn}中是否存在最大项，如果存在，请求出；如果不存在，请说明理由．