题目内容
已知数列{an}的前n项和为Sn,点A(n,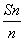 )(n∈N*)总在直线y=
)(n∈N*)总在直线y=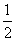 x+
x+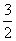 上.
上.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=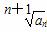 (n∈N*),试问数列{bn}中是否存在最大项,如果存在,请求出;如果不存在,请说明理由.
(n∈N*),试问数列{bn}中是否存在最大项,如果存在,请求出;如果不存在,请说明理由.
(1)因为点A(n,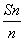 )(n∈N)在直线y=
)(n∈N)在直线y=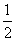 x+
x+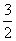 上,
上,
故有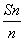 =
=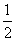 n+
n+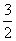 ,即Sn=
,即Sn=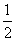 n2+
n2+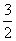 n,
n,
当n≥2时,Sn-1=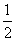 (n-1)2+
(n-1)2+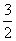 (n-1),
(n-1),
所以an=Sn-Sn-1=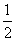 n2+
n2+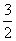 n-[
n-[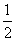 (n-1)2+
(n-1)2+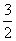 (n-1)]=n+1(n≥2).
(n-1)]=n+1(n≥2).
当n=1时,a1=S1=2满足上式,
故数列{an}的通项公式为an=n+1.
(2)由an=n+1,可知bn=
 所以,b2>b1=b3>b4,
所以,b2>b1=b3>b4,
猜想{bn+1}递减,即猜想当n≥2时,
考察函数y= (x>e),则y′=
(x>e),则y′= ,
,
显然当x>e时,lnx>1,即y′<0,
故y=
猜想正确,因此,数列{bn}的最大项是b2= .
.

练习册系列答案
相关题目
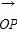 =(2cosx+1,cos2x-sinx+1),
=(2cosx+1,cos2x-sinx+1),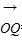 =(cosx,-1),f(x)=
=(cosx,-1),f(x)= ]时,求函数f(x)的最大值及取得最大值时的x值.
]时,求函数f(x)的最大值及取得最大值时的x值. 为{an}的“光阴”值,现知某数列的“光阴”值为Hn=
为{an}的“光阴”值,现知某数列的“光阴”值为Hn= ,则数列{an}的通项公式为________.
,则数列{an}的通项公式为________. ,那么a12=________.
,那么a12=________.