Question

20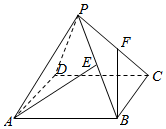．已知正四棱锥P-ABCD中，PA=AB=2，E，F分别是PB，PC的中点，则异面直线AE与BF所成角的余弦值为（　　）

• A． $\frac{{\sqrt{3}}}{3}$
• B． $\frac{{\sqrt{6}}}{3}$
• C． $\frac{1}{6}$
• D． $\frac{1}{2}$

Answer 1

分析 由题意，建立空间直角坐标系，利用数量积公式求向量夹角，得到所求．

解答 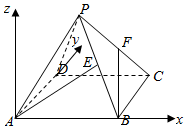解：建立空间直角坐标系如图，设PA=4，则A（0，0，0），B（4，0，0），C（4，4，0），P（2，2，2$\sqrt{2}$）．
所以E（3，1，$\sqrt{2}$），F（3，3，$\sqrt{2}$），所以$\overrightarrow{AE}$=（3，1，$\sqrt{2}$），$\overrightarrow{BF}$=（-1，3，$\sqrt{2}$），
所以异面直线AE与BF所成角的余弦值为：$|\frac{\overrightarrow{AE}•\overrightarrow{BF}}{|\overrightarrow{AE}||\overrightarrow{BF}|}|$=$\frac{1}{6}$；
故选：C．

点评 本题考查了利用空间向量求向量的夹角；关键是正确建系以及正确写出所用向量的坐标，利用数量积公式求夹角．