题目内容
5.已知数列{an}满足${a_n}={2^n}$,则数列{an•bn}满足对任意的n∈N+,都有b1an+b2an-1+…+bna1=${2^n}-\frac{n}{2}-1$,则数列{an•bn}的前n项和Tn=$\frac{(n-1)•{2}^{n}+1}{2}$.分析 对任意的n∈N+,都有b1an+b2an-1+…+bna1=${2^n}-\frac{n}{2}-1$,求得n=1的情况,当n≥2时,将n换为n-1,相减求得bn=$\frac{1}{4}$n,可得an•bn=$\frac{1}{4}$n•2n,再由数列的求和方法:错位相减法,结合等比数列的求和公式,计算即可得到所求和.
解答 解:∵数列{an}满足${a_n}={2^n}$,
由b1an+b2an-1+…+bna1=2n-$\frac{1}{2}$n-1,①
令n=1,则b1a1=2-$\frac{1}{2}$-1,解得b1=$\frac{1}{4}$.
∵b1an+b2an-1+…+bna1=2n-$\frac{1}{2}$n-1,
当n≥2时,b1an-1+b2an-2+…+bn-2a2+bn-1a1=2n-1-$\frac{1}{2}$(n-1)-1,
将上式两边同乘公比2得,b1an+b2an-1+…bn-1a2=2n-n-1.②
①-②可得:bna1=$\frac{1}{2}$n,(n≥2),
由a1=2,可得bn=$\frac{1}{4}$n,对n=1也成立,
则an•bn=$\frac{1}{4}$n•2n,
Tn=$\frac{1}{4}$(1•2+2•22+3•23+…+n•2n),
可得2Tn=$\frac{1}{4}$(1•22+2•23+3•24+…+n•2n+1),
两式相减可得-Tn=$\frac{1}{4}$(2+22+23+24+…+2n-n•2n+1)
=$\frac{1}{4}$($\frac{2(1-{2}^{n})}{1-2}$-n•2n+1),
化简可得Tn=$\frac{(n-1)•{2}^{n}+1}{2}$.
故答案为:$\frac{(n-1)•{2}^{n}+1}{2}$.
点评 本题考查数列递推式的运用和数列的求和方法:错位相减法,考查等比数列的求和公式,以及化简整理的运算能力,属于中档题.

| x | 0 | 1 | 3 | 5 | 6 |
| y | 1 | 2m | 3-m | 3.8 | 9.2 |
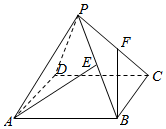 已知正四棱锥P-ABCD中,PA=AB=2,E,F分别是PB,PC的中点,则异面直线AE与BF所成角的余弦值为( )
已知正四棱锥P-ABCD中,PA=AB=2,E,F分别是PB,PC的中点,则异面直线AE与BF所成角的余弦值为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |