题目内容
19．已知集合A={x|$lo{g}_{\frac{1}{2}}$（x-1）＞1}，B={x|x2-2x-3＞0}，则“x∈A”是“x∈B”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 由$lo{g}_{\frac{1}{2}}$（x-1）＞1，可得：$0＜x-1＜\frac{1}{2}$，解得集合A．由x2-2x-3＞0，解得：x＞3，或x＜-1．即可判断出结论．
解答 解：由$lo{g}_{\frac{1}{2}}$（x-1）＞1，可得：$0＜x-1＜\frac{1}{2}$，解得$1＜x＜\frac{3}{2}$，即集合A=$（1，\frac{3}{2}）$．
由x2-2x-3＞0，解得：x＞3，或x＜-1．即B（-∞，-1）∪（3，+∞）．
则“x∈A”是“x∈B”的既不充分也不必要条件．
故选：D．
点评 本题考查了函数的单调性、不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
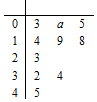已知函数$f（x）={x^2}+\sqrt{2}（m-1）x+\frac{m}{4}$，现有一组数据（数据量较大），从中随机抽取10个，绘制所得的茎叶图如图所示，且茎叶图中的数据的平均数为2．（茎叶图中的数据均为小数，其中茎为整数部分，叶为小数部分）
10．已知实数x，y满足$\left\{\begin{array}{l}{2x-y-2≥0}\\{x+y-1≤0}\\{y+1≥0}\end{array}\right.$，z=mx+y的最大值为3，则实数m的值是（ ）
| A． | -2 | B． | 3 | C． | 8 | D． | 2 |
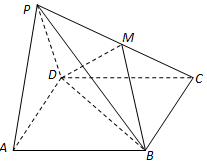如图，在四棱锥P-ABCD中，底面ABCD是矩形，面PAD⊥底面ABCD，且△PAD是边长为2的等边三角形，PC=$\sqrt{13}$，M在PC上，且PA∥面BDM．
8．已知$sin（{α-\frac{π}{3}}）=\frac{{\sqrt{3}}}{3}$，则cos$（{2α+\frac{π}{3}}）$=（ ）
| A． | $\frac{1}{3}$ | B． | $-\frac{1}{3}$ | C． | $-\frac{3}{7}$ | D． | $\frac{3}{7}$ |