题目内容
2．某高级中学高一、高二、高三年级的学生人数分别为600人、700人、700人，为了解不同年级学生的眼睛近视情况，现用分层抽样的方法抽取了容量为100的样本，则高三年级应抽取的学生人数为35．分析 先求出抽样比，由此能求出高三年级应抽取的学生人数．
解答 解：抽样比f=$\frac{100}{600+700+700}$=$\frac{1}{20}$，
∴高三年级应抽取的学生人数为：700×$\frac{1}{20}$=35．
故答案为：35．
点评 本题考查分层抽样的应用，是基础题，解题时要认真审题，注意分层抽样性质的合理运用．
练习册系列答案
相关题目
12．已知函数f（x）=alnx+x2-（a+2）x恰有两个零点，则实数a的取值范围是（ ）
| A． | （-1，+∞） | B． | （-2，0） | C． | （-1，0） | D． | （-2，-1） |
13．某校高二文科100名学生参加了语数英学科竞赛，年级为了解这些学生语文和数学成绩的情况，将100名学生的语文和数学成绩统计如表：
（I）若数学成绩的优秀率为35%，现利用随机抽样从数学成绩“优秀”的学生中抽取1名学生，求该生语文成绩为“及格”的概率；
（II）在语文成绩为“良”的学生中，已知m≥10，n≥10，求数学成绩“优”比“良”的人数少的概率．
| 语文 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 13 | m | 5 |
| 良 | 12 | n | 9 | |
| 及格 | 10 | 14 | 7 | |
（II）在语文成绩为“良”的学生中，已知m≥10，n≥10，求数学成绩“优”比“良”的人数少的概率．
10．已知实数x，y满足$\left\{\begin{array}{l}{2x-y-2≥0}\\{x+y-1≤0}\\{y+1≥0}\end{array}\right.$，z=mx+y的最大值为3，则实数m的值是（ ）
| A． | -2 | B． | 3 | C． | 8 | D． | 2 |
如图所示，等腰梯形ABCD的底角A等于60°．直角梯形ADEF所在的平面垂直于平面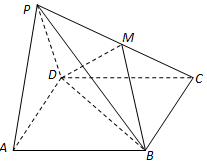
如图，在四棱锥P-ABCD中，底面ABCD是矩形，面PAD⊥底面ABCD，且△PAD是边长为2的等边三角形，PC=$\sqrt{13}$，M在PC上，且PA∥面BDM．
12．若复数z满足iz=1+i，则z的共轭复数$\overline{z}$在复平面内所对应点的坐标为（ ）
| A． | （1，1） | B． | （1，-1） | C． | （-1，1） | D． | （-1，-1） |