题目内容
给出以下命题:
(1)若∫abf(x)dx>0,则f(x)>0;
(2)∫02π|sinx|dx=4;
(3)已知F′(x)=f(x),且F(x)是以T为周期的函数,则∫0af(x)dx=∫Ta+Tf(x)dx;
(4)
dx=
.
其中正确命题的个数为( )
(1)若∫abf(x)dx>0,则f(x)>0;
(2)∫02π|sinx|dx=4;
(3)已知F′(x)=f(x),且F(x)是以T为周期的函数,则∫0af(x)dx=∫Ta+Tf(x)dx;
(4)
| ∫ | +3 -3 |
| 9-x2 |
| 9π |
| 4 |
其中正确命题的个数为( )
| A、1 | B、2 | C、3 | D、0 |
考点:定积分
专题:导数的概念及应用
分析:(1)根据微积分基本定理,得出)∫baf(x)dx=F(b)-F(a)>0,可以看到与f(x)正负无关.
(2)注意到sinx在[0,2π]的取值符号不同,根据微积分基本运算性质,化为∫0πsinxdx+∫π2π(-sinx)dx求解,判断.
(3)根据微积分基本定理,两边分别求解,再结合F(a+T)=F(a),F(T)=F(0)判定.
(4)根据定积分的几何意义,计算可得.
(2)注意到sinx在[0,2π]的取值符号不同,根据微积分基本运算性质,化为∫0πsinxdx+∫π2π(-sinx)dx求解,判断.
(3)根据微积分基本定理,两边分别求解,再结合F(a+T)=F(a),F(T)=F(0)判定.
(4)根据定积分的几何意义,计算可得.
解答:
解:对于(1)由∫baf(x)dx=F(b)-F(a)>0,得F(b)>F(a),未必f(x)>0.故(1)错误.
对于(2))∫02π|sinx|dx=
sinxdx
(-sinx)dx=-cosx
+cosx
=2+2=4,故(2)正确;
对于(3)∫0af(x)dx=F(a)-F(0),∫Ta+Tf(x)dx=F(a+T)-F(T)=F(a)-F(0),则∫0af(x)dx=∫Ta+Tf(x)dx;故(3)正确
对于(4)
dx,表示的面积为圆x2+y2=9的面积的二分之一,故
dx=
×π×32=
,故(4)错误
所以其中正确命题的个数为2个,
故选:B
对于(2))∫02π|sinx|dx=
| ∫ | π 0 |
| +∫ | 2π π |
| | | π 0 |
| | | 2π π |
对于(3)∫0af(x)dx=F(a)-F(0),∫Ta+Tf(x)dx=F(a+T)-F(T)=F(a)-F(0),则∫0af(x)dx=∫Ta+Tf(x)dx;故(3)正确
对于(4)
| ∫ | +3 -3 |
| 9-x2 |
| ∫ | +3 -3 |
| 9-x2 |
| 1 |
| 2 |
| 9π |
| 2 |
所以其中正确命题的个数为2个,
故选:B
点评:本题借助于命题真假的判断与应用,考查微积分基本定理,微积分基本运算性质.属于中档题.

练习册系列答案
相关题目
函数y=xln|x|的大致图象是( )
A、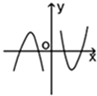 |
B、 |
C、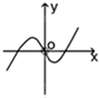 |
D、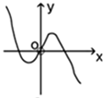 |
设点P在曲线ρsinθ=2上,点Q在曲线ρ=-2cosθ上,则|PQ|的最小值为( )
| A、2 | B、1 | C、3 | D、0 |
关于函数f(x)=sin(2x+
)的四个命题:
①f(x)的图象关于直线x=
对称;
②f(x)的图象关于点(
,0)对称;
③f(x)的最小正周期为π;
④f(x)在[0,
],上为增函数,其中正确的是命题是( )
| π |
| 3 |
①f(x)的图象关于直线x=
| π |
| 12 |
②f(x)的图象关于点(
| π |
| 4 |
③f(x)的最小正周期为π;
④f(x)在[0,
| π |
| 2 |
| A、②③ | B、①② | C、②④ | D、①③ |
已知偶函数f(x)的定义域为R,则下列函数中为奇函数的是( )
| A、sin[f(x)] |
| B、x•f(sinx) |
| C、f(x)•f(sinx) |
| D、[f(sinx)]2 |
角α的终边过点P(-4,3),则sin2α=( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|