题目内容
一个口袋中装有大小和质地都相同的白球和红球共16个，依次从口袋中任取一球，如果取到红球，那么继续取球，且取出的红球不放回；如果取到白球，就停止取球，记取球的次数为随机变量X，若P（X=2）=0.25，则口袋中的白球个数为 ．
考点：古典概型及其概率计算公式
专题：概率与统计
分析：设口袋中白球数为n，由P（X=2）=0.25，得：
=0.25，由此能求出结果．
| ||||
|
解答：
解：（1）设口袋中白球数为n，
则由P（X=2）=0.25，得：
=0.25，
即n（16-n）=60，解得n=10或n=6，
故答案为：10或6．
则由P（X=2）=0.25，得：
| ||||
|
即n（16-n）=60，解得n=10或n=6，
故答案为：10或6．
点评：本题考查概率的求法，是基础题，解题时要认真审题，注意排列组合知识的灵活运用．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
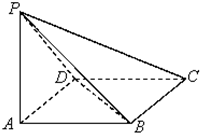如图，已知四棱锥P-ABCD，侧棱PA⊥平面ABCD，底面ABCD为菱形，∠DAB=60°且PA=AB，则直线AB与平面PBC所成角的正弦值为