题目内容
在△ABC中，内角A，B，C所对应的边分别是a，b，c，若c2=（a-b）2+6，C=
，则△ABC的面积是
．
| π |
| 3 |
考点：余弦定理,正弦定理
专题：综合题,解三角形
分析：利用余弦定理，结合c2=（a-b）2+6，C=
，求出ab=6，利用S△ABC=
absinC，求出△ABC的面积．
| π |
| 3 |
| 1 |
| 2 |
解答：
解：由c2=（a-b）2+6，可得c2=a2+b2-2ab+6，
由余弦定理：c2=a2+b2-2abcosC=a2+b2-ab=a2+b2-ab，
所以：a2+b2-2ab+6=a2+b2-ab，
所以ab=6；
所以S△ABC=
absinC=
×6×
=
．
故答案为：
．
由余弦定理：c2=a2+b2-2abcosC=a2+b2-ab=a2+b2-ab，
所以：a2+b2-2ab+6=a2+b2-ab，
所以ab=6；
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
故答案为：
3
| ||
| 2 |
点评：本题考查余弦定理，正弦定理的运用，考查学生的计算能力，确定ab=6是关键．
练习册系列答案
相关题目
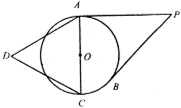如图，半径为1的圆O外有一动点P，过P作圆O的切线PA，PB切于点A，B，以直径AC为一边作正三角形△ADC，则
如图是一个平面图形的直观图，在直观图中，O′C′=O′D′=2，O′A′=3，则原平面图形的面积为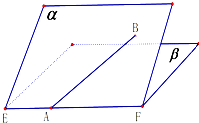
如图，二面角α-EF-β的大小是60°，线段AB?α，A在EF上，AB与β所成的角为30°，则sin∠BAF=f（x）=
则f[f（
）]=（ ）
|
| 1 |
| 4 |
| A、9 | ||
B、
| ||
| C、1 | ||
| D、3 |
若函数f（x）=lnx+2x2-ax存在与直线2x-y=0平行的切线，则实数a取值范围是（ ）
| A、（-∞，-6] |
| B、（-∞，-6]∪[2，+∞） |
| C、[2，+∞） |
| D、（-∞，-6）∪（2，+∞） |