题目内容
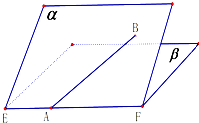如图，二面角α-EF-β的大小是60°，线段AB?α，A在EF上，AB与β所成的角为30°，则sin∠BAF=考点：二面角的平面角及求法
专题：空间角
分析：过B作BO⊥β，作出二面角和AB与β所成的角为30°，根据三角形的边角关系即可得到结论．
解答：
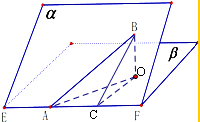解：过B作BO⊥β，过O作OC⊥AF于C，连结BC，AO，
则BC⊥AF，
即∠BCO是二面角α-EF-β的大小，即∠BCO=60°，
∠BAO是AB与β所成的角，即∠BAO=30°，
则sin∠BAF=
，
∵sin∠BCO=sin60°=
=
，sin∠BAO=sin30°
=
，
∴
BC=
AB，即
=
，
则sin∠BAF=
=
，
故答案为：
解：过B作BO⊥β，过O作OC⊥AF于C，连结BC，AO，则BC⊥AF，
即∠BCO是二面角α-EF-β的大小，即∠BCO=60°，
∠BAO是AB与β所成的角，即∠BAO=30°，
则sin∠BAF=
| BC |
| AB |
∵sin∠BCO=sin60°=
| BO |
| BC |
| ||
| 2 |
| BO |
| AB |
| 1 |
| 2 |
∴
| ||
| 2 |
| 1 |
| 2 |
| BC |
| AB |
| ||
| 3 |
则sin∠BAF=
| BC |
| AB |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题主要考查空间二面角和线面角的求解和计算，根据空间角的定义，作出空间角是解决本题的关键．
练习册系列答案
相关题目
等差数列{an}的前n项和记为Sn，若a2+a4+a6的值为一确定的常数，则下列各数中也是常数的是（ ）
| A、S7 |
| B、S8 |
| C、S13 |
| D、S15 |
椭圆
+
=1（a＞b＞0）的左右焦点分别为F1，F2，若其上存在一点Q使得∠F1QF2=120°，则其离心率的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、（0，1） | ||||
B、[
| ||||
C、[
| ||||
D、[
|