题目内容
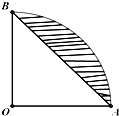 如图扇形
如图扇形 |
| AOB |
A、1-
| ||||
B、1-
| ||||
C、
| ||||
D、
|
考点:几何概型
专题:概率与统计
分析:根据题意,分别算出弓形面积和扇形面积,再利用几何概型公式加以计算,即可得到所求概率.
解答:
解:∵扇形
中,OA⊥OB,OA=1,
∴阴影部分的面积为
-
,扇形的面积为
,
∴豆子落在阴影部分的概率为
=1-
.
故选:A.
 |
| AOB |
∴阴影部分的面积为
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
∴豆子落在阴影部分的概率为
| ||||
|
| 2 |
| π |
故选:A.
点评:本题给出丢豆子的事件,求豆子落入指定区域的概率.着重考查了弓形、扇形面积公式和几何概型的计算等知识,属于基础题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
下列各数中最小的一个是( )
| A、111111(2) |
| B、210(6) |
| C、1000(4) |
| D、101(8) |
对任意的实数t,直线ty=x-
与圆x2+y2=1的位置关系一定是( )
| 1 |
| 2 |
| A、相切 |
| B、相交且直线不过圆心 |
| C、相交且直线不一定过圆心 |
| D、相离 |
 定义在R上的奇函数f(x)在[0,+∞)上的图象如图所示,则不等式(2013x-1)f(x)<0的解集是
定义在R上的奇函数f(x)在[0,+∞)上的图象如图所示,则不等式(2013x-1)f(x)<0的解集是