题目内容
某旅游公司有客房300间，每间房租为200元，每天客满，公司欲提高档次，并提高租金．如果每间客房每日增加20元，客房出租就减少10间，若不考虑其他因素，公司将房租提高到多少时，每天客房的租金总收入最高？
考点：根据实际问题选择函数类型
专题：函数的性质及应用
分析：根据如果每间客房每日增加20元，客房出租就减少10间，可求每天客房的租金收入，确定函数的对称轴，即可求最值．
解答：
解：设公司将房租提高x个20元，则每天客房的租金收入y为：
y=（200+20x）（300-10x）=60000+4000x-200x2 （x∈N）
这个二次函数图象的对称轴为：x=-
=10，
所以当x=10时，y最大值=80000，200+20x=200+20×10=400．
答：将房租提高到400元/间时，客房的租金总收入最高，每天为80000元．
y=（200+20x）（300-10x）=60000+4000x-200x2 （x∈N）
这个二次函数图象的对称轴为：x=-
| 4000 |
| 2×(-200) |
所以当x=10时，y最大值=80000，200+20x=200+20×10=400．
答：将房租提高到400元/间时，客房的租金总收入最高，每天为80000元．
点评：本题考查利用数学知识解决实际问题，考查二次函数的最值，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
已知cos（
-α）=
，
＜a＜π，则sin（α+
）=（ ）
| π |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
在直角坐标系中，角α以x轴非负半轴为始边，终边上有一点P（3，4），则cosα=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）是R上的偶函数，对?x∈R都有f(x+2)=
，且当x∈[0，2）时，f（x）=log2（x+1），则f（-2013）+f（2015）的值等于（ ）
| 1 |
| f(x) |
| A、-2 | B、-1 | C、1 | D、2 |
已知全集U=R，集合A={x|1＜x＜4}，B={x|x≥2}，则A∩∁UB=（ ）
| A、{x|1＜x≤2} |
| B、{x|2＜x＜4} |
| C、{x|1＜x＜2} |
| D、{x|x＜2} |
设偶函数f（x）对任意x∈R都有f（x）=-
且当x∈[-3，-2]时f（x）=4x，则f（119.5）=（ ）
| 1 |
| f(x-3) |
| A、10 | ||
| B、-10 | ||
C、
| ||
D、-
|
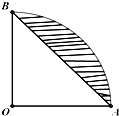如图扇形 |
| AOB |
A、1-
| ||||
B、1-
| ||||
C、
| ||||
D、
|