题目内容
对任意的实数t,直线ty=x-
与圆x2+y2=1的位置关系一定是( )
| 1 |
| 2 |
| A、相切 |
| B、相交且直线不过圆心 |
| C、相交且直线不一定过圆心 |
| D、相离 |
考点:直线与圆的位置关系
专题:直线与圆
分析:对任意的实数t,直线ty=x-
恒过定点(
,0),判断定点(
,0)在圆内,即可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:对任意的实数t,直线ty=x-
恒过定点(
,0),
∵(
)2+02<1,
∴定点(
,0)在圆内,
∵(0,0)不在直线ty=x-
上,
∴对任意的实数t,直线ty=x-
与圆x2+y2=1的位置关系一定是相交且直线不过圆心.
故选B.
| 1 |
| 2 |
| 1 |
| 2 |
∵(
| 1 |
| 2 |
∴定点(
| 1 |
| 2 |
∵(0,0)不在直线ty=x-
| 1 |
| 2 |
∴对任意的实数t,直线ty=x-
| 1 |
| 2 |
故选B.
点评:本题考查直线与圆的位置关系,考查直线恒过定点,确定直线过定点是关键.

练习册系列答案
相关题目
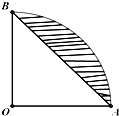 如图扇形
如图扇形 |
| AOB |
A、1-
| ||||
B、1-
| ||||
C、
| ||||
D、
|