题目内容
下列各数中最小的一个是（ ）
| A、111111（2） |
| B、210（6） |
| C、1000（4） |
| D、101（8） |
考点：进位制,排序问题与算法的多样性
专题：计算题
分析：欲找四个中最小的数，先将它们分别化成十进制数，后再比较它们的大小即可．
解答：
解：111111（2）=25+24+23+22+21+20=63；
210（6）=2×62+1×6=78；
1000（4）=1×43=64；
101（8）=1×82+1=65．
故11111（2）最小，
故选：A．
210（6）=2×62+1×6=78；
1000（4）=1×43=64；
101（8）=1×82+1=65．
故11111（2）最小，
故选：A．
点评：本题考查的知识点是算法的概念，由n进制转化为十进制的方法，我们只要依次累加各位数字上的数×该数位的权重，即可得到结果．属于基础题．
练习册系列答案
相关题目
设偶函数f（x）对任意x∈R都有f（x）=-
且当x∈[-3，-2]时f（x）=4x，则f（119.5）=（ ）
| 1 |
| f(x-3) |
| A、10 | ||
| B、-10 | ||
C、
| ||
D、-
|
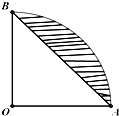如图扇形 |
| AOB |
A、1-
| ||||
B、1-
| ||||
C、
| ||||
D、
|
下列函数为奇函数的是（ ）
A、f（x）=
| ||
| B、f（x）=-|x+1| | ||
C、f（x）=（
| ||
| D、f（x）=lg（x+1） |