题目内容
已知a,b均为正实数,
是3a与3b的等比中项,则
+
的最小值是 .
| 3 |
| 1 |
| a |
| 2 |
| b |
考点:基本不等式在最值问题中的应用,等比数列的通项公式
专题:不等式的解法及应用
分析:利用
是3a与3b的等比中项,可得a+b=1,再代入,利用基本不等式,即可求最值.
| 3 |
解答:
解:∵
是3a与3b的等比中项,
∴3=3a•3b,
∴3=3a+b,
∴a+b=1,
∴
+
=(
+
)(a+b)=3+
+
≥3+2
=3+2
,
当且仅当
=
时取等号,
∴
+
的最小值是3+2
.
故答案为:3+2
.
| 3 |
∴3=3a•3b,
∴3=3a+b,
∴a+b=1,
∴
| 1 |
| a |
| 2 |
| b |
| 1 |
| a |
| 2 |
| b |
| b |
| a |
| 2a |
| b |
|
| 2 |
当且仅当
| b |
| a |
| 2a |
| b |
∴
| 1 |
| a |
| 2 |
| b |
| 2 |
故答案为:3+2
| 2 |
点评:本题考查等比数列的性质,考查基本不等式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知函数f(x)是R上的偶函数,对?x∈R都有f(x+2)=
,且当x∈[0,2)时,f(x)=log2(x+1),则f(-2013)+f(2015)的值等于( )
| 1 |
| f(x) |
| A、-2 | B、-1 | C、1 | D、2 |
袋中标号为1,2,3,4的四只球,四人从中各取一只,其中甲不取1号球,乙不取2号球,丙不取3号球,丁不取4号球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知等差数列{an}的前n项和Sn,若a4=18-a5,则S8=__________( )
| A、18 | B、36 | C、54 | D、72 |
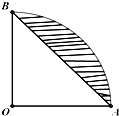 如图扇形
如图扇形 |
| AOB |
A、1-
| ||||
B、1-
| ||||
C、
| ||||
D、
|
下列函数为奇函数的是( )
A、f(x)=
| ||
| B、f(x)=-|x+1| | ||
C、f(x)=(
| ||
| D、f(x)=lg(x+1) |