题目内容
已知一个空间几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的体积为 ．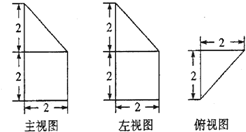
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由已知中的三视图可知，该几何体是一个三棱锥和三棱柱结合而成的组合体，分别求出三棱锥和三棱柱的体积，相加可得答案．
解答：
解：由三视图可知，该几何体是一个三棱锥和三棱柱形成的组合体，
其中棱锥和棱柱的底面积均为直角边长为2的等腰直角三角形，
故S=
×2×2=2，
棱锥和棱柱的高h均为2，
故组合体的体积V=Sh+
Sh=
×2×2=
，
故答案为：
．
其中棱锥和棱柱的底面积均为直角边长为2的等腰直角三角形，
故S=
| 1 |
| 2 |
棱锥和棱柱的高h均为2，
故组合体的体积V=Sh+
| 1 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
故答案为：
| 16 |
| 3 |
点评：本题考查的知识点是由三视图求体积，其中根据已知中的三视图分析出几何体的形状是解答的关键．
练习册系列答案
应用题作业本系列答案
相关题目
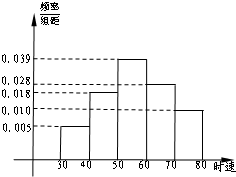5000辆汽车经过某一雷达测速区，其速度频率分布直方图如图所示，则时速超过70km/h的汽车数量为（ ）| A、50 | B、500 |
| C、1000 | D、4500 |
已知椭圆C：
+
=1（a＞b＞0）的右焦点是F，上顶点是A，点M满足
=
(
+
)（O为坐标原点），且sin∠MAF=
，则椭圆C的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| AM |
| 1 |
| 2 |
| AO |
| AF |
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设向量
=（x，0），
=（x-2，1），集合A={x|
•
≥0}，B={x|0＜x＜4}，则A∩B=（ ）
| a |
| b |
| a |
| b |
| A、[2，4） |
| B、（2，4） |
| C、（-∞，4） |
| D、（-∞，0] |