题目内容
19.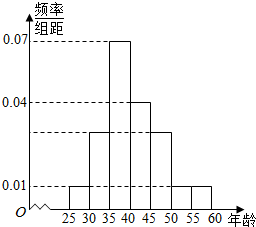 某校对该校的1000名教师的年龄进行统计分析,年龄的频率分布直方图如图所示.规定年龄[25,40)的为青年教师,年龄[40,50)为中年教师,年龄在[50,60)为老年教师.
某校对该校的1000名教师的年龄进行统计分析,年龄的频率分布直方图如图所示.规定年龄[25,40)的为青年教师,年龄[40,50)为中年教师,年龄在[50,60)为老年教师.(I)求年龄[30,35)、[40,45)的教师人数;
(Ⅱ)现用分层抽样的方法从中、青年中抽取18人进行课堂展示,求抽到年龄在[35,40)的人数.
(Ⅲ)在(Ⅱ)中抽取的中年教师中,随机选取2名教师进行总结交流,求抽取的中年教师中甲、乙至少有一名作总结交流的概率.
分析 (I)根据频率=$\frac{频数}{样本容量}$,求出对应的频率与频数;
(Ⅱ)根据分层抽样原理,计算出从中青年教师中抽取的18人年龄在[35,40)中的人数;
(Ⅲ)利用列举法求出从7名教师中随机选取2名的可能情况,计算甲、乙至少有1名作总结交流的概率.
解答 解:(I)年龄在[40,45)的教师人数为1000×0.04×5=200人;
年龄在[30,35)的教师频率为$\frac{1}{2}$[1-(0.07+0.04+0.03)×5]=0.15
年龄在[30,35)的教师人数为1000×0.15=150人;
(Ⅱ)中青年教师共有1000×(1-0.02×5)=900,
其中年龄在[35,40)中有1000×0.07×5=350人,
设抽取的18人年龄在[35,40)中的有x人,
则18:900=x:350,解得x=7;
(Ⅲ)中年教师共350人,所以抽出的18人中,中年教师有7人,
不妨设7名教师分别为甲、乙、A、B、C、D、E,
从7人中随机选取2名教师的可能情况有
甲乙,甲A,甲B,甲C,甲D,甲E,乙A,乙B,乙C,乙D,乙E,
AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共21种,
其中甲乙至少有1人有11种情况,
所以抽取的中年教师中甲、乙至少有一名作总结交流的概率为$\frac{11}{21}$.
点评 本题考查了频率分布直方图的应用问题,也考查了用列举法求古典概型的概率问题,是基础题目.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
9.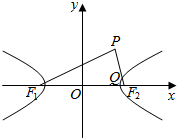 如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,点P在第一象限,且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$,($\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,点P在第一象限,且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$,($\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
 如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,点P在第一象限,且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$,($\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,点P在第一象限,且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$,($\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )| A. | y=±$\frac{\sqrt{5}}{5}x$ | B. | y=±$\frac{1}{2}x$ | C. | y=±$\frac{\sqrt{3}}{2}x$ | D. | y=±$\frac{\sqrt{3}}{3}x$ |
10.已知命题P:?x∈R,mx2+1<1;q:?x∈R,x2+mx+1≥0,若p∨(¬q)为假命题,则实数m的取值范围是( )
| A. | (-∞,0)∪(2,+∞) | B. | [0,2] | C. | [2,+∞) | D. | [-2,0] |
7.平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,$\overrightarrow{a}$=(2,0),|$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$-2$\overrightarrow{b}$|=( )
| A. | $2\sqrt{3}$ | B. | 0 | C. | $\sqrt{6}$ | D. | 2 |
4.以F(1,0)为焦点的抛物线的标准方程是( )
| A. | x=4y2 | B. | y=4x2 | C. | x2=4y | D. | y2=4x |



