题目内容
9.已知数列{an}是公差为d的等差数列;(1)若a1+1,a3+3,a5+5构成等比数列,求d的值;
(2)在(1)题条件下,若a1=3,设bn=an•($\frac{1}{2}$)n,数列{bn}前n项和为Sn,求证:$\frac{3}{2}$≤Sn≤$\frac{17}{8}$.
分析 (1)a1+1,a3+3,a5+5构成等比数列,可得$({a}_{3}+3)^{2}$=(a1+1)(a5+5),即$({a}_{1}+2d+3)^{2}$=(a1+1)(a1+4d+5),解得d.
(2)an=3-(n-1)=4-n,bn=an•($\frac{1}{2}$)n=(4-n)$•(\frac{1}{2})^{n}$,利用“错位相减法”与等比数列的前n项和公式即可得出Sn.再利用数列的单调性即可得出.
解答 (1)解:∵a1+1,a3+3,a5+5构成等比数列,∴$({a}_{3}+3)^{2}$=(a1+1)(a5+5),
∴$({a}_{1}+2d+3)^{2}$=(a1+1)(a1+4d+5),化为(d+1)2=0,解得d=-1.
(2)证明:an=3-(n-1)=4-n,
∴bn=an•($\frac{1}{2}$)n=(4-n)$•(\frac{1}{2})^{n}$,
∴Sn=$3×\frac{1}{2}$+2×$(\frac{1}{2})^{2}$+…+$(4-n)•(\frac{1}{2})^{n}$,
$\frac{1}{2}{S}_{n}$=$3×(\frac{1}{2})^{2}$+2×$(\frac{1}{2})^{3}$+…+(5-n)$•(\frac{1}{2})^{n}$+(4-n)•$(\frac{1}{2})^{n+1}$,
∴$\frac{1}{2}{S}_{n}$=$3×\frac{1}{2}$-$[(\frac{1}{2})^{2}+(\frac{1}{2})^{3}+…+(\frac{1}{2})^{n}]$-(4-n)•$(\frac{1}{2})^{n+1}$=$\frac{3}{2}$-$\frac{\frac{1}{4}[1-(\frac{1}{2})^{n-1}]}{1-\frac{1}{2}}$-(4-n)•$(\frac{1}{2})^{n+1}$=1+(n-2)×$(\frac{1}{2})^{n+1}$,
∴Sn=2+(n-2)×$(\frac{1}{2})^{n}$.∵Sn+1-Sn=$(2+\frac{n-1}{{2}^{n+1}})$-$(2+\frac{n-2}{{2}^{n}})$=$\frac{3-n}{{2}^{n+1}}$,
∴当1≤n≤3时,数列{Sn}是单调递增数列,当n≥4时,数列{Sn}是单调递减数列.
即S1<S2<S3=S4>S5>S6…,
又$\frac{3}{2}$=S1<S2=2,且n≥3,Sn>2.
∴Sn的最小值为$\frac{3}{2}$;当n=3或4时,Sn的最大值为$\frac{17}{8}$.
故:$\frac{3}{2}$≤Sn≤$\frac{17}{8}$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“错位相减法”、数列的单调性,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案| A. | 36 | B. | 35 | C. | 34 | D. | 33 |
| A. | {0,1} | B. | {-1,1} | C. | {1} | D. | {-1,0,1} |
表1:
| x | 1 | 2 | 3 | 4 | 5 |
| y | 2.9 | 3.3 | 3.6 | 4.4 | 5.1 |
| u | 1 | 2 | 3 | 4 | 5 |
| v | 25 | 20 | 21 | 15 | 13 |
| A. | 变量x与y正相关,u与v正相关 | B. | 变量x与y负相关,u与v正相关 | ||
| C. | 变量x与y负相关,u与v负相关 | D. | 变量x与y正相关,u与v负相关 |
已知喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
(1)请将上面的列联表补充完整;
(2)能否在犯错误的概率不超过0.005的前提下认为喜好体育运动与性别有关?说明你的理由;
| 喜好体育运动 | 不喜好体育运动 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
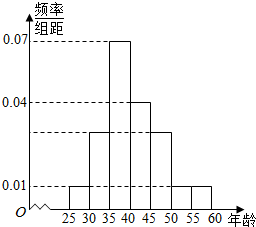 某校对该校的1000名教师的年龄进行统计分析,年龄的频率分布直方图如图所示.规定年龄[25,40)的为青年教师,年龄[40,50)为中年教师,年龄在[50,60)为老年教师.
某校对该校的1000名教师的年龄进行统计分析,年龄的频率分布直方图如图所示.规定年龄[25,40)的为青年教师,年龄[40,50)为中年教师,年龄在[50,60)为老年教师.