题目内容
7.平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,$\overrightarrow{a}$=(2,0),|$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$-2$\overrightarrow{b}$|=( )| A. | $2\sqrt{3}$ | B. | 0 | C. | $\sqrt{6}$ | D. | 2 |
分析 根据向量的模的计算和向量的数量积的运算即可求出答案.
解答 解:∵平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,$\overrightarrow{a}$=(2,0),|$\overrightarrow{b}$|=1,
∴|$\overrightarrow{a}$|=2,
|$\overrightarrow{a}$-2$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+4|$\overrightarrow{b}$|2-4$\overrightarrow{a}$•$\overrightarrow{b}$=4+4-4×2×1•cos$\frac{π}{3}$=4,
∴|$\overrightarrow{a}$-2$\overrightarrow{b}$|=2,
故选:D.
点评 本题考查了向量的模的计算和向量的数量积的运算,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知集合A={-1,1},B={x|x∈R,1≤2x≤4},则A∩B等于( )
| A. | {0,1} | B. | {-1,1} | C. | {1} | D. | {-1,0,1} |
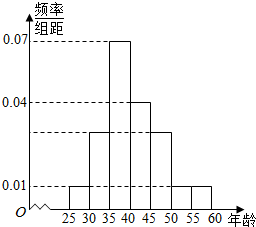 某校对该校的1000名教师的年龄进行统计分析,年龄的频率分布直方图如图所示.规定年龄[25,40)的为青年教师,年龄[40,50)为中年教师,年龄在[50,60)为老年教师.
某校对该校的1000名教师的年龄进行统计分析,年龄的频率分布直方图如图所示.规定年龄[25,40)的为青年教师,年龄[40,50)为中年教师,年龄在[50,60)为老年教师.