题目内容
10.已知命题P:?x∈R,mx2+1<1;q:?x∈R,x2+mx+1≥0,若p∨(¬q)为假命题,则实数m的取值范围是( )| A. | (-∞,0)∪(2,+∞) | B. | [0,2] | C. | [2,+∞) | D. | [-2,0] |
分析 根据复合函数的真假关系,确定命题p,q的真假,利用函数的性质分别求出对应的取值范围即可得到结论.
解答 解:命题p:?x∈R,mx2+1<1即mx2<0,
∴m<0时p是真命题,
m≥0时p是假命题;
对于q::?x∈R,x2+mx+1≥0,
则△=m2-4≤0,解得-2≤m≤2,
若p∨(?q)为假命题,则p,?q为假命题,
即p是假命题,q是真命题,
∴$\left\{\begin{array}{l}{m≥0}\\{-2≤m≤2}\end{array}\right.$,解得:0≤m≤2
故选:B.
点评 本题主要考查复合命题之间的关系,利用函数的性质求出相应的取值范围是解决本题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
1.对a,b∈R,记min{a,b}=$\left\{\begin{array}{l}{a,a≤b}\\{b,a>b}\end{array}\right.$,函数f(x)=min{-|x|,-x2+4x+6}的最大值是( )
| A. | 6 | B. | 1 | C. | 0 | D. | $\frac{3-\sqrt{33}}{2}$ |
20.已知数列{an}的前n项和为${S_n}={n^2}-2n$,则a3+a17=( )
| A. | 36 | B. | 35 | C. | 34 | D. | 33 |
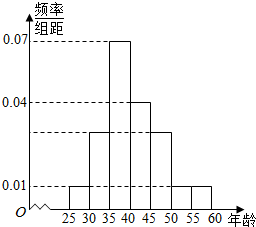 某校对该校的1000名教师的年龄进行统计分析,年龄的频率分布直方图如图所示.规定年龄[25,40)的为青年教师,年龄[40,50)为中年教师,年龄在[50,60)为老年教师.
某校对该校的1000名教师的年龄进行统计分析,年龄的频率分布直方图如图所示.规定年龄[25,40)的为青年教师,年龄[40,50)为中年教师,年龄在[50,60)为老年教师.