题目内容
设A={x|x2-|x-2|-4≤0},B={x|x2-(2m+1)x+2m<0}.
(Ⅰ)化简集合A;
(Ⅱ)若A∩B=B,求实数m的取值范围.
(Ⅰ)化简集合A;
(Ⅱ)若A∩B=B,求实数m的取值范围.
考点:交集及其运算
专题:集合
分析:(Ⅰ)根据绝对值性质,分段化简集合A;
(Ⅱ)由A∩B=B得B是A的子集,利用包含关系可得关于m的不等式(组).
(Ⅱ)由A∩B=B得B是A的子集,利用包含关系可得关于m的不等式(组).
解答:
解:(Ⅰ)由x2-|x-2|-4≤0,得|x-2|≥x2-4,
∴x-2≥x2-4或x-2≤4-x2,即(x-2)(x+1)≤0或(x-2)(x+3)≤0,
解得:-1≤x≤2或-3≤x≤2,
∴-3≤x≤2,
∴A=[-3,2];
(Ⅱ)由x2-(2m+1)x+2m<0,得(x-1)(x-2m)<0,
分两种情况考虑:
①若2m=1,即m=
,则B=∅,满足A∩B=B;
②若2m>1,即m>
,则B=(1,2m),
∵A∩B=B,
∴2m≤2,即m≤1,
∴
<m≤1;
③若2m<1,即m<
,则B=(2m,1),
∵A∩B=B,
∴2m≥-3,即m≥-
,
∴-
≤m<
,
由①②③可知实数m的取值范围是[-
,1].
∴x-2≥x2-4或x-2≤4-x2,即(x-2)(x+1)≤0或(x-2)(x+3)≤0,
解得:-1≤x≤2或-3≤x≤2,
∴-3≤x≤2,
∴A=[-3,2];
(Ⅱ)由x2-(2m+1)x+2m<0,得(x-1)(x-2m)<0,
分两种情况考虑:
①若2m=1,即m=
| 1 |
| 2 |
②若2m>1,即m>
| 1 |
| 2 |
∵A∩B=B,
∴2m≤2,即m≤1,
∴
| 1 |
| 2 |
③若2m<1,即m<
| 1 |
| 2 |
∵A∩B=B,
∴2m≥-3,即m≥-
| 3 |
| 2 |
∴-
| 3 |
| 2 |
| 1 |
| 2 |
由①②③可知实数m的取值范围是[-
| 3 |
| 2 |
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
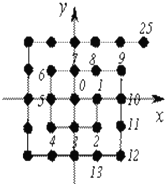 将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,…,点(0,1)处标7,…,依此类推,则标签20152的格点的坐标为( )
将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,…,点(0,1)处标7,…,依此类推,则标签20152的格点的坐标为( )| A、(1008,1007) |
| B、(1007,1006) |
| C、(1007,1005) |
| D、(1006,1005) |
函数y=
的定义域为( )
| log2(2x2-x) |
A、{x|x≤-
| ||
B、{x|x<-
| ||
C、{x|x≤0,或x≥
| ||
D、{x|x<0,或x>
|
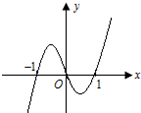 已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),则以下说法错误的是( )
已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),则以下说法错误的是( )| A、f′(1)+f′(-1)=0 |
| B、当x=-1时,函数f(x)取得极大值 |
| C、方程xf'(x)=0与f(x)=0均有三个实数根 |
| D、当x=1时,函数f(x)取得极小值 |
