题目内容
已知直线l:x-2ycosα+3=0(α∈[
,
]),则直线l的倾斜角的取值范围为 .
| π |
| 6 |
| π |
| 3 |
考点:直线的倾斜角,直线的一般式方程
专题:直线与圆
分析:求出直线的斜率,求出斜率的范围,转化为 倾斜角的正切值的范围,即可求解倾斜角的范围.
解答:
解:由题意,α∈[
,
],cosα∈[
,
],设直线l的倾斜角为θ;
可得tanθ=
∵-1≤cosθ≤1且cosθ≠0,cosα∈[
,
],
∈[
,1]
∴tanθ∈[
,1],
∵0≤θ<π,∴结合正切函数的单调性,可得
≤θ≤
,
直线l的倾斜角θ的取值范围是:[
,
]
故答案为:[
,
].
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
可得tanθ=
| 1 |
| 2cosα |
∵-1≤cosθ≤1且cosθ≠0,cosα∈[
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2cosα |
| ||
| 3 |
∴tanθ∈[
| ||
| 3 |
∵0≤θ<π,∴结合正切函数的单调性,可得
| π |
| 6 |
| π |
| 4 |
直线l的倾斜角θ的取值范围是:[
| π |
| 6 |
| π |
| 4 |
故答案为:[
| π |
| 6 |
| π |
| 4 |
点评:本题给出直线方程含有余弦函数系数的形式,求直线倾斜角范围,着重考查了余弦函数的值域和正切函数的单调性等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

多面体的三视图如图所示,则该多面体的表面积为(单位:cm)( )
A、28+4
| ||
B、30+4
| ||
C、30+4
| ||
D、28+4
|
在锐角△ABC中,∠A=2∠B,则
的取值范围为( )
| c |
| b |
| A、[1,2] |
| B、[1,3] |
| C、(1,3) |
| D、(1,2) |
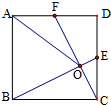 如图,在正方形ABCD中,E.F分别是CD.DA的中点,BE交CF于点O,若
如图,在正方形ABCD中,E.F分别是CD.DA的中点,BE交CF于点O,若