题目内容
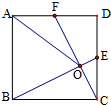如图，在正方形ABCD中，E．F分别是CD．DA的中点，BE交CF于点O，若| AO |
| BE |
| CF |
| λ |
| μ |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：可以选正方形边上的向量来表示向量
：
=(
+
)
+k
，
=t
+(1-
)
，所以根据平面向量基本定理即可得到
，所以解出t=
，这样即可用
，
表示
=
+
，而
=(λ-
)
-(
+μ)
，所以得到
，解出λ，μ即可得到
．
| AO |
| AO |
| 1 |
| 2 |
| k |
| 2 |
| AD |
| DC |
| AO |
| AD |
| t |
| 2 |
| DC |
|
| 4 |
| 5 |
| AD |
| DC |
| AO |
| 4 |
| 5 |
| AD |
| 3 |
| 5 |
| DC |
| AO |
| μ |
| 2 |
| AD |
| λ |
| 2 |
| DC |
|
| λ |
| μ |
解答：
解：
=
+
；
F，O，C三点共线，存在实数k使
=k
=k(
+
)；
∴
=
+k(
+
)=(
+
)
+k
；
同理，
=
+
=t
+(1-
)
，t∈R；
∴
，解得t=
；
∴
=
+
；
又
=λ
+μ
=(λ-
)
-(
+μ)
；
∴
，解得
；
∴
=-
．
故答案为：-
．
| AO |
| AF |
| FO |
F，O，C三点共线，存在实数k使
| FO |
| FC |
| 1 |
| 2 |
| AD |
| DC |
∴
| AO |
| 1 |
| 2 |
| AD |
| 1 |
| 2 |
| AD |
| DC |
| 1 |
| 2 |
| k |
| 2 |
| AD |
| DC |
同理，
| AO |
| AB |
| BO |
| AD |
| t |
| 2 |
| DC |
∴
|
| 4 |
| 5 |
∴
| AO |
| 4 |
| 5 |
| AD |
| 3 |
| 5 |
| DC |
又
| AO |
| BE |
| CF |
| μ |
| 2 |
| AD |
| λ |
| 2 |
| DC |
∴
|
|
∴
| λ |
| μ |
| 1 |
| 2 |
故答案为：-
| 1 |
| 2 |
点评：考查向量的加法运算，以及共线向量基本定理，相等向量，相反向量，平面向量基本定理．
练习册系列答案
相关题目
已知等差数列{an}中，有
+1＜0，且它们的前n项和Sn有最大值，则使得Sn＞0的n的最大值为（ ）
| a2014 |
| a2013 |
| A、4024 | B、4025 |
| C、4026 | D、4027 |
执行如图所示的程序框图，输出的S值是（ ）| A、13 | B、14 | C、15 | D、16 |
