题目内容
如图,已知一个正三棱锥P-ABC的底面棱长AB=3,高PO=
,求这个正三棱锥的表面积.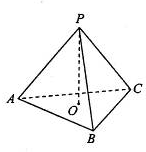
| 6 |

考点:棱柱、棱锥、棱台的侧面积和表面积
专题:计算题,空间位置关系与距离
分析:连接AO,确定正三棱锥P-ABC的四个面是全等的等边三角形,即可求这个正三棱锥的表面积.
解答:
解:连接AO,在等边三角形ABC中,由AB=3,可得AO=
=
,
在Rt△AOP中,AP=
=3,
∴正三棱锥P-ABC的四个面是全等的等边三角形,
∴S表面积=4×
×32=9
.
| 2 |
| 3 |
32-(
|
| 3 |
在Rt△AOP中,AP=
| 3+6 |
∴正三棱锥P-ABC的四个面是全等的等边三角形,
∴S表面积=4×
| ||
| 4 |
| 3 |
点评:本题主要考查基本运算,考查三棱锥的全面积,属于中档题.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
已知函数f(x)=
,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是( )
|
| A、a<0 | B、a≤0 |
| C、a<3 | D、0<a<3 |
已知f(x)=sin(2014x+
)+cos(2014x-
)的最大值为A,若存在实数x1,x2,使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1-x2|的最小值为( )
| π |
| 6 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某三棱锥的三视图如图所示,则该三棱锥的体积是( )


| A、1 | ||
B、
| ||
C、
| ||
D、
|
在△ABC中,若
=
=
,则△ABC的形状是( )
| a | ||
cos
|
| b | ||
cos
|
| c | ||
cos
|
| A、直角三角形 |
| B、等腰非等边三角形 |
| C、等边三角形 |
| D、等腰直角三角形 |