题目内容
19.已知函数f(x)=(2-a)lnx+$\frac{1}{x}$+2ax(a≤0).(Ⅰ)当a=0时,求f(x)的极值;
(Ⅱ)当a<0时,讨论f(x)的单调性;
(Ⅲ)若对任意的a∈(-3,-2)及x1,x2∈[1,3],恒有(m+ln3)a-2ln3>|f(x1)-f(x2)|成立,求实数m的取值范围.
分析 (Ⅰ)当a=0时,$f(x)=2lnx+\frac{1}{x}$,定义域为(0,+∞),求出f(x)的导函数.判断导函数的符号,推出导函数的单调性,然后求解极值、
(Ⅱ)当a<0时,$f(x)=(2-a)lnx+\frac{1}{x}+2ax$的定义域为(0,+∞),求出f(x)的导函数,由f′(x)=0得极值点,通过(1)当-2<a<0时,(2)当a=-2时,(3)当a<-2时,分别求解函数的单调区间即可.
解答 解:(Ⅰ)当a=0时,$f(x)=2lnx+\frac{1}{x}$,定义域为(0,+∞),
f(x)的导函数${f^'}(x)=\frac{2}{x}-\frac{1}{x^2}=\frac{2x-1}{x^2}$.
当$0<x<\frac{1}{2}$时,f′(x)<0,f(x)在$(0,\frac{1}{2})$上是减函数;
当$x>\frac{1}{2}$时,f′(x)>0,f(x)在$(\frac{1}{2},+∞)$上是增函数.
∴当$x=\frac{1}{2}$时,f(x)取得极小值为$f(\frac{1}{2})=2-2ln2$,无极大值.
(Ⅱ)当a<0时,$f(x)=(2-a)lnx+\frac{1}{x}+2ax$的定义域为(0,+∞),f(x)的导函数为${f^'}(x)=\frac{2-a}{x}-\frac{1}{x^2}+2a=\frac{{2a{x^2}+(2-a)x-1}}{x^2}=\frac{(2x-1)(ax+1)}{x^2}$.
由f′(x)=0得${x_1}=\frac{1}{2}>0$,${x_2}=-\frac{1}{a}>0$,${x_1}-{x_2}=\frac{1}{2}-(-\frac{1}{a})=\frac{a+2}{2a}$.
(1)当-2<a<0时,f(x)在$(0,\frac{1}{2})$上是减函数,在$(\frac{1}{2},-\frac{1}{a})$上是增函数,在$(-\frac{1}{a},+∞)$上是减函数;
(2)当a=-2时,f(x)在(0,+∞)上是减函数;
(3)当a<-2时,f(x)在$(0,-\frac{1}{a})$上是减函数,在$(-\frac{1}{a},\frac{1}{2})$上是增函数,
在$(\frac{1}{2},+∞)$上是减函数.
综上所述,
当a<-2时,f(x)在$(0,-\frac{1}{a}),(\frac{1}{2},+∞)$上是减函数,在$(-\frac{1}{a},\frac{1}{2})$上是增函数;
当a=-2时,f(x)在(0,+∞)上是减函数;
当-2<a<0时,f(x)在$(0,\frac{1}{2}),(-\frac{1}{a},+∞)$上是减函数,在$(\frac{1}{2},-\frac{1}{a})$上是增函数.
(Ⅲ)由(Ⅱ)知,当a∈(-∞,-2)时,f(x)在[1,3]上是减函数.
∴$|f({x_1})-f({x_2})|≤f(1)-f(3)=\frac{2}{3}-4a+(a-2)ln3$.
∵对于任意的x1,x2∈[1,3],a∈(-∞,-2)都有|f(x1)-f(x2)|<(m+ln3)a-2ln3,
∴$\frac{2}{3}-4a+(a-2)ln3<(m+ln3)a-2ln3$对任意a<-2恒成立,
∴$m<-4+\frac{2}{3a}$对任意a<-2恒成立.
当a<-2时,$-\frac{13}{3}<-4+\frac{2}{3a}<-4$,∴$m≤-\frac{13}{3}$.
∴实数m的取值范围为$(-∞,-\frac{13}{3}]$.
点评 本题考查函数的导数的综合应用,函数的极值以及函数的单调性的判断以及考查分类讨论思想转化思想的应用.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案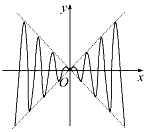 如图,虚线部分是平面直角坐标系四个象限的角平分线,实线部分是函数y=f(x)的部分图象,则f(x)可能是( )
如图,虚线部分是平面直角坐标系四个象限的角平分线,实线部分是函数y=f(x)的部分图象,则f(x)可能是( )| A. | x2sinx | B. | xsinx | C. | x2cosx | D. | xcosx |
| A. | 1 | B. | 2 | C. | 4 | D. | 0 |
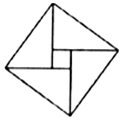 第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如下图会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么$sin({θ+\frac{π}{3}})$=$\frac{{4+3\sqrt{3}}}{10}$.
第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如下图会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么$sin({θ+\frac{π}{3}})$=$\frac{{4+3\sqrt{3}}}{10}$.