题目内容
7.已知f(x)=xlnx,g(x)=-x2+ax-3.(1)求函数f(x)在(0,+∞)上的最小值;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.
分析 (1)求出x>0,f′(x)=lnx+1,利用导数性质能求出求函数f(x)在(0,+∞)上的最小值.
(2)2xlnx≥-x2+ax-3恒成立,等价于$a≤x+2lnx+\frac{3}{x}$恒成立,记$h(x)=x+2lnx+\frac{3}{x}(x>0)$,则${h}^{'}(x)=\frac{{x}^{2}+2x-3}{{x}^{2}}$,利用导数性质能求出实数a的取值范围.
解答 解:(1)∵f(x)=xlnx,
∴x>0,f′(x)=lnx+1,
由f′(x)>0,得x>$\frac{1}{e}$,∴f(x)在$(\frac{1}{e},+∞)$上单调递增,
由f′(x)<0,得0<x<$\frac{1}{e}$,∴f(x)在$(0,\frac{1}{e})$上单调递减,
∴f(x)在$x=\frac{1}{e}$处取最小值,
∴$f{(x)_{min}}=f(\frac{1}{e})=\frac{1}{e}ln\frac{1}{e}=-\frac{1}{e}$.
(2)2xlnx≥-x2+ax-3恒成立,等价于$a≤x+2lnx+\frac{3}{x}$恒成立,
记$h(x)=x+2lnx+\frac{3}{x}(x>0)$,
则${h}^{'}(x)=\frac{{x}^{2}+2x-3}{{x}^{2}}$=$\frac{(x+3)(x-1)}{{x}^{2}}$,
当x∈(0,1)时,h′(x)<0,当x∈(1,+∞)时,h′(x)>0,
∴h(x)在(0,1)内单调递减,在(1,+∞)内单调递增,
∴h(x)min=h(1)=4,
∴实数a的取值范围是(-∞,4].
点评 本题考查函数值的最小值的求法,考查实数的取值范围的求法,考查导数的应用,考查推理论证能力、运算求解能力,考查转化化归思想、分类讨论思想,是中档题.

| A. | $({\frac{1}{3},\frac{1}{2}})$ | B. | $({\frac{1}{3},\frac{1}{2}})∪({1,+∞})$ | C. | (1,+∞) | D. | $({\frac{1}{3},1})∪({1,+∞})$ |
| A. | “x<1”是“log2(x+1)<1”的充分不必要条件 | |
| B. | 命题“?x>0,2x>1”的否定是“$?{x_0}≤0,{2^{x_0}}≤1$” | |
| C. | 命题“若a≤b,则ac2≤bc2”的逆命题为真命题 | |
| D. | 命题“若a+b≠5,则a≠2或b≠3”为真命题. |
| A. | p是假命题 | B. | q是真命题 | C. | (¬q)是真命题 | D. | (¬p)∧q是真命题 |
| A. | 1 | B. | -1 | C. | 2 | D. | $\frac{1}{2}$ |
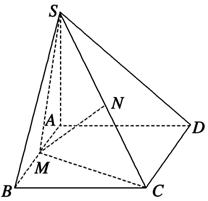 如图所示,在四棱锥S-ABCD中,AD∥BC,AD⊥AB,CD⊥平面SAD,SA=AD=2,AB=1,SB=$\sqrt{5}$,SD=2$\sqrt{2}$,M,N分别为AB,SC的中点.
如图所示,在四棱锥S-ABCD中,AD∥BC,AD⊥AB,CD⊥平面SAD,SA=AD=2,AB=1,SB=$\sqrt{5}$,SD=2$\sqrt{2}$,M,N分别为AB,SC的中点.