题目内容
2.(x+1)2($\frac{1}{x}$-1)5的展开式中常数项为( )| A. | 21 | B. | 19 | C. | 9 | D. | -1 |
分析 本题是两个多项式的乘法运算,要求运算结果中的常数项,注意第一个多项式的三项,要想得到常数必需是和约分以后得到常数的项相乘,写出二项式中的三项,相乘再相加,即可得出结论.
解答 解:∵(x+1)2($\frac{1}{x}$-1)5=(x2+2x+1)($\frac{1}{x}$-1)5,
根据二项式定理可知,($\frac{1}{x}$-1)5展开式的通项公式为${C}_{5}^{r}$•(-1)r•xr-5,
∴(x+1)2($\frac{1}{x}$-1)5的展开式中常数项由三部分构成,
分别是(x2+2x+1)与($\frac{1}{x}$-1)5展开式中各项相乘得到,
令r=3,则${C}_{5}^{3}$•(-1)3•x-2,则1×(-${C}_{5}^{3}$)=-10;
令r=4,则${C}_{5}^{4}$•(-1)4•x-1,则2×${C}_{5}^{4}$=10;
令r=5,则${C}_{5}^{5}$•(-1)5•x0,则1×(-1)=-1;
所以常数项为-10+10-1=-1.
故选:D.
点评 本题考查了求二项式展开式的常数项的应用问题,在解题过程中应用多项式乘以多项式的法则,是易错题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
13.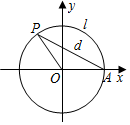 如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π
如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π
 如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π
如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π| A. | 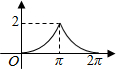 | B. | 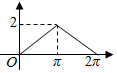 | C. |  | D. | 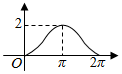 |
17.下列命题中,真命题的个数是( )
①经过直线外一点有且只有一条直线与已知直线平行
②经过直线外一点有且只有一条直线与已知直线垂直
③经过平面外一点有且只有一个平面与已知平面平行
④经过平面外一点有且只有一个平面与已知平面垂直.
①经过直线外一点有且只有一条直线与已知直线平行
②经过直线外一点有且只有一条直线与已知直线垂直
③经过平面外一点有且只有一个平面与已知平面平行
④经过平面外一点有且只有一个平面与已知平面垂直.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.下列命题中正确的是( )
| A. | 若ξ服从正态分布N(0,2),且P(ξ>2)=0.4,则P(0<ξ<2)=0.2 | |
| B. | x=1是x2-x=0的必要不充分条件 | |
| C. | 直线ax+y+2=0与ax-y+4=0垂直的充要条件为a=±1 | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
14.若正实数m、n满足3m+4n=5mn,则m+3n的最小值是( )
| A. | 4 | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{28}{5}$ |
11.设全集U={x∈N|x≥1},集合A={x∈N|x2≥3},则∁UA=( )
| A. | ∅ | B. | {1} | C. | {1,2} | D. | {1,2,3} |
12.已知集合A={x|(x+1)(x-2)≤0},B={x|x-1>0},则A∩B=( )
| A. | [-2,1) | B. | (1,+∞) | C. | (1,2] | D. | (2,+∞) |