题目内容
12.以直角坐标系的原点O为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度.设圆C:$\left\{\begin{array}{l}{x=\sqrt{2}cosθ}\\{y=\sqrt{2}sinθ}\end{array}\right.$(θ为参数)上的点到直线l:ρcos(θ-$\frac{π}{4}$)=$\sqrt{2}$k的距离为d.①当k=3时,求d的最大值;
②若直线l与圆C相交,试求k的取值范围.
分析 ①当k=3时,可化l的方程为x+y-6=0,由点到直线的距离公式和三角函数的最值可得;
②分别化为普通方程x2+y2=2,x+y-k=0,由直线l与圆C相交可得圆心O到直线l的距离d<$\sqrt{2}$,解关于k的不等式可得.
解答 解:①当k=3时,l:ρcos(θ-$\frac{π}{4}$)=3$\sqrt{2}$,
可得l:ρcosθcos$\frac{π}{4}$+ρsinθsin$\frac{π}{4}$=3$\sqrt{2}$,
整理得l:x+y-6=0,
则d=$\frac{|\sqrt{2}cosθ+\sqrt{2}sinθ-6|}{\sqrt{2}}$=$\frac{|2sin(θ+\frac{π}{4})-6|}{\sqrt{2}}$
∴当sin(θ+$\frac{π}{4}$)=-1时,dmax=$\frac{8}{\sqrt{2}}$=4$\sqrt{2}$;
②消去cosθ可将圆C的参数方程化为普通方程x2+y2=2,
直线l的极坐标方程化为普通方程x+y-k=0,
∵直线l与圆C相交,∴圆心O到直线l的距离d<$\sqrt{2}$,
即$\frac{|-k|}{\sqrt{2}}$<$\sqrt{2}$,解得-2<k<2.
点评 本题考查参数方程和极坐标方程,涉及点到直线的距离公式以及直线和圆的位置关系,属中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
2.若a是$\sqrt{3}$的整数部分,b是$\sqrt{3}$的小数部分,则(a+$\frac{1}{b}$)6展开式的中间项是( )
| A. | 25+15$\sqrt{3}$ | B. | 20+3$\sqrt{15}$ | C. | 15+3$\sqrt{3}$ | D. | 22+3$\sqrt{15}$ |
7.一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值.
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,求这8个数据的方差.
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
(1)求z的值.
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,求这8个数据的方差.
17.若复数z满足(1+i)(z+1)+1-i=0,则复数$\overline z$所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是夹角为60°的两个单位向量,若$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$+λ$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=2$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$,$\overrightarrow{a}⊥\overrightarrow{b}$,则λ=( )
| A. | $\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{2}$ | D. | 2 |
2.(x+1)2($\frac{1}{x}$-1)5的展开式中常数项为( )
| A. | 21 | B. | 19 | C. | 9 | D. | -1 |
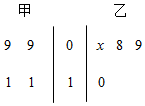 从甲、乙两个班级分别抽取4名同学的年龄制作出如右图所示的茎叶图,乙班的记录中有一个数据模糊,无法确认,在图中以X表示,已知这8个同学的平均年龄是9.5岁.
从甲、乙两个班级分别抽取4名同学的年龄制作出如右图所示的茎叶图,乙班的记录中有一个数据模糊,无法确认,在图中以X表示,已知这8个同学的平均年龄是9.5岁.