题目内容
19.函数y=log3(2x-1)的定义域为( )| A. | (1,+∞) | B. | $({\frac{1}{2},1})$ | C. | [1,+∞) | D. | $({\frac{1}{2},+∞})$ |
分析 根据对数函数的定义,真数大于0,列出不等式求出解集即可.
解答 解:∵函数y=log3(2x-1),
∴2x-1>0,
解得x>$\frac{1}{2}$;
∴函数y的定义域为($\frac{1}{2}$,+∞).
故选:D.
点评 本题考查了求对数函数定义域的应用问题,是基础题目.

练习册系列答案
相关题目
10.执行如图所示的程序框图,若输出的n=6,则输入整数p的最小值是.( )


| A. | 17 | B. | 16 | C. | 18 | D. | 19 |
11.执行如图的程序框图,若输入a0=4,a1=-1,a2=3,a3=-2,a4=1,则输出的t的值为( )
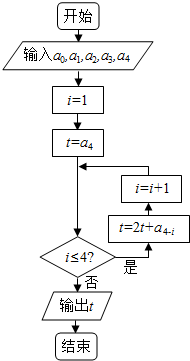

| A. | 5 | B. | 10 | C. | 12 | D. | 14 |
8.执行如图的程序框图,若输入k=100,则输出的n=( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
9.设U=R,集合A={x|x>0},集合B={x|lgx>0},则A∩(∁UB)=( )
| A. | {x|0≤x<1} | B. | {x|0<x≤1} | C. | {x|x<0} | D. | {x|x>1} |