题目内容

7．已知（1+2i）$\overline z$=4+3i（其中i是虚数单位，$\overline z$是z 的共轭复数），则z的虚部为（　　）
A．1B．-1C．iD．-i

分析 利用复数的运算法则、共轭复数的定义、虚部的定义即可得出．

解答 解：∵（1+2i）$\overline z$=4+3i，
∴$\overline{z}$=$\frac{4+3i}{1+2i}$=$\frac{（4+3i）（1-2i）}{（1+2i）（1-2i）}$=$\frac{10-5i}{5}$=2-i，
∴z=2+i，
∴z的虚部为1．
故选：A．

点评 本题考查了复数的运算法则、共轭复数的定义、虚部的定义，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
17．若f（x）在x=x0处的导数存在，则当h→0时 $\frac{f（{x}_{0}+h）-f（{x}_{0}-h）}{2h}$等于（　　）
A．2 f′（x0）B．$\frac{1}{2}$ f′（x0）C．f′（x0）D．4 f′（x0）
18．执行如图所示的程序框图，如果输入a=-1，b=-2，则输出的a的值为（　　）
A．16B．8C．4D．2
15．根据如图所示的伪代码，如果输入x的值为0，则输出结果y为5．
2．一个算法的程序框图如图，若该程序输出的结果为$\frac{5}{6}$，则判断框中的条件i＜m中的整数m的值是6．
12．执行如图所示的程序框图，输出的S值为（　　）
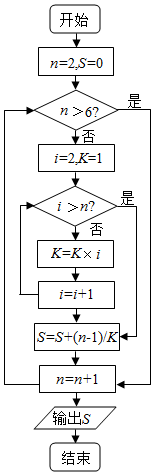
A．$\frac{119}{120}$B．$\frac{359}{360}$C．$\frac{719}{720}$D．$\frac{5039}{5040}$
19．函数y=log3（2x-1）的定义域为（　　）
A．（1，+∞）B．$（{\frac{1}{2}，1}）$C．[1，+∞）D．$（{\frac{1}{2}，+∞}）$
16．设函数f（x）=$\sqrt{lnx+x+a}$，若曲线y=$\frac{e-1}{2}$sinx+$\frac{e+1}{2}$上存在点（x0，y0）使得f（f（y0））=y0成立，则实数a的取值范围为（　　）
A．[0，e2-e+1]B．[0，e2+e-1]C．[0，e2-e-1]D．[0，e2+e+1]
17．篮球运动员乙在某几场比赛中得分的茎叶图如图所示，则他在这几场比赛中得分的中位数为（　　）
A．26B．27C．26.5D．27.5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网