题目内容
14.设某人有5发子弹,他向某一目标射击时,每发子弹命中目标的概率为$\frac{2}{3}$,若他连续两发命中或连续两发不中则停止射击,否则将子弹打完.(Ⅰ)求他前两发子弹只命中一发的概率;
(Ⅱ)求他所耗用的子弹数X的分布列与期望.
分析 (Ⅰ)利用互斥事件概率加法公式和相互独立事件乘法概率公式能求出他前两发子弹只命中一发的概率.
(Ⅱ)由已知得他所耗用的子弹数X的可能取值为2,3,4,5,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)∵某人有5发子弹,他向某一目标射击时,每发子弹命中目标的概率为$\frac{2}{3}$,
∴他前两发子弹只命中一发的概率:
p=$\frac{2}{3}×(1-\frac{2}{3})+(1-\frac{2}{3})×\frac{2}{3}$=$\frac{4}{9}$.
(Ⅱ)由已知得他所耗用的子弹数X的可能取值为2,3,4,5,
P(X=2)=($\frac{2}{3}$)2+($\frac{1}{3}$)2=$\frac{5}{9}$,
P(X=3)=$\frac{1}{3}×(\frac{2}{3})^{2}+\frac{2}{3}×(\frac{1}{3})^{2}$=$\frac{2}{9}$,
P(X=4)=$\frac{2}{3}×\frac{1}{3}×(\frac{2}{3})^{2}+\frac{1}{3}×\frac{2}{3}×(\frac{1}{3})^{2}$=$\frac{10}{81}$,
P(X=5)=$\frac{1}{3}×\frac{2}{3}×\frac{1}{3}×(\frac{2}{3})^{2}+\frac{2}{3}×\frac{1}{3}×\frac{2}{3}×(\frac{1}{3})^{2}$+$\frac{1}{3}×\frac{2}{3}×\frac{1}{3}×\frac{2}{3}×\frac{1}{3}$+$\frac{2}{3}×\frac{1}{3}×\frac{2}{3}×\frac{1}{3}×\frac{2}{3}$=$\frac{8}{81}$,
∴X的分布列为:
| X | 2 | 3 | 4 | 5 |
| P | $\frac{5}{9}$ | $\frac{2}{9}$ | $\frac{10}{81}$ | $\frac{8}{81}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

 阅读快车系列答案
阅读快车系列答案| A. | (5x)'=5x | B. | (5x)'=5xln5 | C. | $({log_a}x)'=\frac{lna}{x}$ | D. | .$({log_a}x)'=\frac{a}{x}$ |
| A. | (1,+∞) | B. | $({\frac{1}{2},1})$ | C. | [1,+∞) | D. | $({\frac{1}{2},+∞})$ |
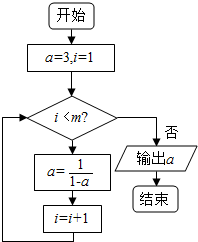
| A. | 3 | B. | -$\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 2 |

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
