题目内容
下列说法:
(1)命题“?x∈R,2x≤0”的否定是“?x∈R,2x>0”;
(2)关于x的不等式a<sin2x+
恒成立,则a的取值范围是a<3;
(3)对于函数f(x)=
(a∈R且a≠0),则有当a=1时,?k∈(1,+∞),使得函数g(x)=f(x)-kx在R上有三个零点;
(4)
dx≤
dx;
(5)已知m,n,s,t∈R+,m+2n=5,
+
=9,n>m,且m,n是常数,又s+2t的最小值是1,则m+3n=7.
其中正确的个数是 .
(1)命题“?x∈R,2x≤0”的否定是“?x∈R,2x>0”;
(2)关于x的不等式a<sin2x+
| 2 |
| sin2x |
(3)对于函数f(x)=
| ax |
| 1+|x| |
(4)
| ∫ | 1 0 |
| 1-x2 |
| ∫ | e 1 |
| 1 |
| x |
(5)已知m,n,s,t∈R+,m+2n=5,
| m |
| s |
| n |
| t |
其中正确的个数是
考点:命题的真假判断与应用,命题的否定,定积分
专题:计算题,简易逻辑
分析:利用特称命题的真假判断(1)的正误;通过函数的最值求出a的范围判断(2)的正误;利用函数的零点集合函数的图象判断(3)的正误;利用定积分求出结果判断(4)的正误;根据s+2t的最小值是 1,根据均值不等式求得的最下值,进而求得此时的m+3n的值即可判断正误;
解答:
解:对于(1),命题“?x∈R,2x≤0”的否定是“?x∈R,2x>0”;满足命题的否定形式,∴(1)正确;
对于(2),关于x的不等式a<sin2x+
恒成立,可得a小于sin2x+
的最小值,sin2x+
+
≥2
+
=2+
≥3,当且仅当sin2x=1时取得最大值,∴(2)正确;
对于(3),∵g(0)=f(0)-0=0,∴x=0是函数g(x)的一个零点;
当x>0时,若?k∈(1,+∞),使得函数g(x)=f(x)-kx在区间(0,+∞)上有零点,则方程
-kx=0必有解,此方程化为kx=1-k,
∵x=
<0,∴此方程无解,∴不存在k∈(1,+∞),使得函数g(x)=f(x)-kx在区间(0,+∞)上有零点;
同理不存在k∈(1,+∞),使得函数g(x)=f(x)-kx在区间(-∞,0)上有零点,故(3)不正确;
对于(4),
dx,由定积分的几何意义可得:
dx=
;
dx=lnx
=1,
∴
dx≤
dx,正确;
对于(5),∵(s+2t)(
+
)=m+2n+
+
≥m+2n+2
=m+2n+2
,(2t2m=s2n时取等号)∴m+2n+2
=9,
∴mn=2,得m=1,n=2得点m+3n=7.∴(5)正确;
正确命题的个数是4个.
故答案为:4.
对于(2),关于x的不等式a<sin2x+
| 2 |
| sin2x |
| 2 |
| sin2x |
| 1 |
| sin2x |
| 1 |
| sin2x |
sin2x•
|
| 1 |
| sin2x |
| 1 |
| sin2x |
对于(3),∵g(0)=f(0)-0=0,∴x=0是函数g(x)的一个零点;
当x>0时,若?k∈(1,+∞),使得函数g(x)=f(x)-kx在区间(0,+∞)上有零点,则方程
| x |
| 1+x |
∵x=
| 1-k |
| k |
同理不存在k∈(1,+∞),使得函数g(x)=f(x)-kx在区间(-∞,0)上有零点,故(3)不正确;
对于(4),
| ∫ | 1 0 |
| 1-x2 |
| ∫ | 1 0 |
| 1-x2 |
| π |
| 4 |
| ∫ | e 1 |
| 1 |
| x |
| | | e 1 |
∴
| ∫ | 1 0 |
| 1-x2 |
| ∫ | e 1 |
| 1 |
| x |
对于(5),∵(s+2t)(
| m |
| s |
| n |
| t |
| 2tm |
| s |
| sn |
| t |
|
| 2mn |
| 2mn |
∴mn=2,得m=1,n=2得点m+3n=7.∴(5)正确;
正确命题的个数是4个.
故答案为:4.
点评:本题考查命题的真假的判断,定积分以及函数的零点、基本不等式、命题的否定,库存基本知识的应用.

练习册系列答案
相关题目
已知向量
、
满足|
|=1,|
|=
,且(3
-2
)⊥
,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
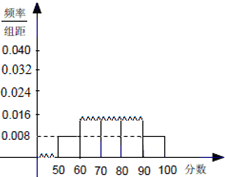 随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是:[50,60),2;[60,70),7;[70,80),10;[80,90),x;[90,100],2.其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题.
随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是:[50,60),2;[60,70),7;[70,80),10;[80,90),x;[90,100],2.其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题.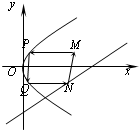 如图,从点M(x0,4)发出的光线,沿平行于抛物线y2=8x的对称轴方向射向此抛物线上的点P,经抛物线反射后,穿过焦点射向抛物线上的点Q,再经抛物线反射后射向直线l:x-y-10=0上的点N,经直线反射后又回到点M,则x0等于( )
如图,从点M(x0,4)发出的光线,沿平行于抛物线y2=8x的对称轴方向射向此抛物线上的点P,经抛物线反射后,穿过焦点射向抛物线上的点Q,再经抛物线反射后射向直线l:x-y-10=0上的点N,经直线反射后又回到点M,则x0等于( )