题目内容
下列四个命题中正确的命题序号是( )
①向量
,
共线的充分必要条件是存在唯一实数λ,使
=λ
成立.
②函数y=f(x-1)与y=f(1-x)的图象关于直线x=1对称.
③ysinθ-cosθ=2y(θ∈[0,π])成立的充分必要条件是|2y|≤
.
④已知U为全集,则x∉A∩B的充分条件是x∈(∁UA)∩(∁UB).
①向量
| a |
| b |
| a |
| b |
②函数y=f(x-1)与y=f(1-x)的图象关于直线x=1对称.
③ysinθ-cosθ=2y(θ∈[0,π])成立的充分必要条件是|2y|≤
| 1+y2 |
④已知U为全集,则x∉A∩B的充分条件是x∈(∁UA)∩(∁UB).
| A、②④ | B、①② | C、①③ | D、③④ |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用向量共线定理即可判断出;
②利用平移变换即可得出;
③利用两角和差的正弦公式和正弦函数的单调性有界性及其充分必要条件即可判断出;
④利用集合的运算即可判断出.
②利用平移变换即可得出;
③利用两角和差的正弦公式和正弦函数的单调性有界性及其充分必要条件即可判断出;
④利用集合的运算即可判断出.
解答:
解:①向量
,
共线的充分必要条件是存在唯一实数λ,使
=λ
成立,当
=
,
≠
时,不存在实数λ.
可知不正确.
②∵函数y=f(x-1)的图象是将函数y=f(x)的图象向右平移一个单位得到,而y=f(1-x)的图象是把函数y=f(x)先关于y轴对称得出y=f(-x),再将此函数的图象向右平移一个单位得到,因此函数y=f(x-1)与y=f(1-x)的图象关于直线x=1对称,故正确;
③由ysinθ-cosθ=2y(θ∈[0,π])可化为
sin(θ-φ)=2y,即sin(θ-φ)=
.
则由sin(θ-φ)=
成立可得|2y|≤
;
反之不成立,因为|2y|≤
成立,也可能sin(θ-φ)=
成立.
因此|2y|≤
是ysinθ-cosθ=2y(θ∈[0,π])成立必要非充分条件,因此不正确.
④已知U为全集,∵(∁UA)∩(∁UB)=CU(A∪B).
∴x∉A∩B的充分条件是x∈(∁UA)∩(∁UB).故正确.
综上可知:只有②④正确.
故选:A.
| a |
| b |
| a |
| b |
| b |
| 0 |
| a |
| 0 |
可知不正确.
②∵函数y=f(x-1)的图象是将函数y=f(x)的图象向右平移一个单位得到,而y=f(1-x)的图象是把函数y=f(x)先关于y轴对称得出y=f(-x),再将此函数的图象向右平移一个单位得到,因此函数y=f(x-1)与y=f(1-x)的图象关于直线x=1对称,故正确;
③由ysinθ-cosθ=2y(θ∈[0,π])可化为
| y2+1 |
| 2y | ||
|
则由sin(θ-φ)=
| 2y | ||
|
| 1+y2 |
反之不成立,因为|2y|≤
| 1+y2 |
| -2y | ||
|
因此|2y|≤
| 1+y2 |
④已知U为全集,∵(∁UA)∩(∁UB)=CU(A∪B).
∴x∉A∩B的充分条件是x∈(∁UA)∩(∁UB).故正确.
综上可知:只有②④正确.
故选:A.
点评:本题考查了向量共线定理、平移变换及其对称性、两角和差的正弦公式和正弦函数的单调性有界性、集合的运算等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
已知向量
、
满足|
|=1,|
|=
,且(3
-2
)⊥
,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
 任意画一个正方形,再将这个正方形各边的中点相连得到第二个正方形,依此类推,这样一共画了3个正方形,如图所示.若向图形中随机投一点,则所投点落在第三个正方形的概率是( )
任意画一个正方形,再将这个正方形各边的中点相连得到第二个正方形,依此类推,这样一共画了3个正方形,如图所示.若向图形中随机投一点,则所投点落在第三个正方形的概率是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
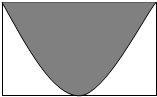 如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60颗豆子落在阴影部分内,则用随机摸拟的方法可以估计图中阴影部分的面积为( )
如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60颗豆子落在阴影部分内,则用随机摸拟的方法可以估计图中阴影部分的面积为( ) 如图所示,一游泳者自游泳池边AB上的D点,沿DC方向游了10米,∠CDB=60°,然后任意选择一个方向并沿此方向继续游,则他再游不超过10米就能够回到游泳池AB边的概率是( )
如图所示,一游泳者自游泳池边AB上的D点,沿DC方向游了10米,∠CDB=60°,然后任意选择一个方向并沿此方向继续游,则他再游不超过10米就能够回到游泳池AB边的概率是( )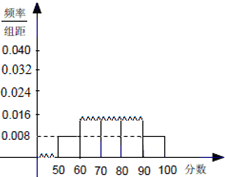 随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是:[50,60),2;[60,70),7;[70,80),10;[80,90),x;[90,100],2.其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题.
随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是:[50,60),2;[60,70),7;[70,80),10;[80,90),x;[90,100],2.其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题. 如图,从点M(x0,4)发出的光线,沿平行于抛物线y2=8x的对称轴方向射向此抛物线上的点P,经抛物线反射后,穿过焦点射向抛物线上的点Q,再经抛物线反射后射向直线l:x-y-10=0上的点N,经直线反射后又回到点M,则x0等于( )
如图,从点M(x0,4)发出的光线,沿平行于抛物线y2=8x的对称轴方向射向此抛物线上的点P,经抛物线反射后,穿过焦点射向抛物线上的点Q,再经抛物线反射后射向直线l:x-y-10=0上的点N,经直线反射后又回到点M,则x0等于( )