在△ABC中.a=$\sqrt{2}$.b=$\sqrt{3}$.B=60°.求角A.角C和边c．题目和参考答案——青夏教育精英家教网——

题目内容

4．在△ABC中，a=$\sqrt{2}$、b=$\sqrt{3}$、B=60°，求角A，角C和边c．

分析直接利用正弦定理求出A的正弦值，利用大边对大角可求A为锐角，从而可求A的值，利用三角形内角和定理可求C的值，进而利用正弦定理可求c的值．

解答（本题满分12分）
解：∵a=$\sqrt{2}$、b=$\sqrt{3}$、B=60°，
∴sinA=$\frac{a•sinB}{b}$=$\frac{\sqrt{2}×\frac{\sqrt{3}}{2}}{\sqrt{3}}$=$\frac{\sqrt{2}}{2}$，
∵a＜b，A为锐角，
∴A=45°，C=180°-A-B=75°，
∴c=$\frac{a•sinC}{sinA}$=$\frac{\sqrt{2}×sin（30°+45°）}{\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{2}+\sqrt{6}}{2}$．

点评本题主要考查了正弦定理，大边对大角，三角形内角和定理在解三角形中的综合应用，考查计算能力和转化思想，属于基础题．

练习册系列答案

数理报系列答案

培优竞赛新方法系列答案

素养提升讲练系列答案

数学指导系列答案

导学与训练系列答案

导与学学案导学系列答案

地道中考系列答案

地理图册系列答案

第一测评系列答案

点金系列答案

相关题目

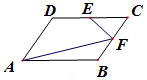如图，菱形ABCD的边长为1，∠DAB=60°，E，F分别为DC、BC的中点，则$\overrightarrow{AF}•\overrightarrow{EF}$=$\frac{1}{8}$．

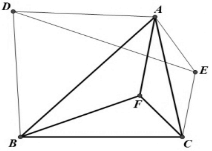已知，△ABC内有一点F，分别以AB、AC为底边向外作等腰三角形DAB、AEC，且∠BAD=∠BCF，∠ACE=∠CBF．求证：DE平分AF．

12．已知平面向量$\vec a，\vec b，\vec c$满足$|\vec a|=1，\vec a•\vec b=\vec b•\vec c=1，\vec a•\vec c=2$，则$|\vec a+\vec b+\vec c|$的最小值是4．

19．已知函数f（x）=|x-a²-a|，不等式f（x）≥$\frac{3}{2}$的解集为{x|x≤$\frac{1}{2}$或x≥$\frac{7}{2}$}．
（1）求实数a的值；
（2）若f（x）+f（x+2）≥m²-m对任意x∈R恒成立，求实数m的取值范围．

9．已知p：|2x+1|≤3，q：x²-2x+1-m²≤0（m＞0），若￢p是￢q的必要不充分条件，求实数m的取值范围．

16．作出下列函数图象，并按照要求答题．
（1）$f（x）=\frac{x+1}{x}$；
（2）f（x）=x²-4|x|．

（1）值域为：（-∞，1）∪（1，+∞）
（2）单调增区间为：（-2，0）∪（2．+∞）．

13．过双曲线$C：\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$的右焦点F作x轴的垂线，交双曲线C于M、N两点，A为左顶点，这∠MAN=θ，双曲线C的离心率为f（θ），则$f（\frac{2π}{3}）-f（\frac{π}{3}）$=$\frac{2\sqrt{3}}{3}$．

14．如果函数f（x）为奇函数，当x＜0时，f（x）=ln（-x）+3x，则曲线在点（1，3）处的切线方程为（　　）

y+3=-2（x-1）