题目内容
6.若点A($\sqrt{3}$,1)的直线l1:$\sqrt{3}$x+ay-2=0与过点B($\sqrt{3}$,4)的直线l2交于点C,若△ABC是以AB为底边的等腰三角形,则l2的方程为( )| A. | $\sqrt{3}$x+y-7=0 | B. | $\sqrt{3}$x-y+7=0 | C. | x+$\sqrt{3}$y-7=0 | D. | x-$\sqrt{3}$y-7=0 |
分析 把点A代入直线l1求出a的值,求出直线l1的斜率,再根据等腰三角形的性质可得l2的斜率,根据点斜式求出直线方程即可
解答 解:过点的直线点A($\sqrt{3}$,1)
∴3+a-2=0,解得a=-1;
∴直线l1的斜率为$\sqrt{3}$;
∵△ABC是以AB为底边的等腰三角形,
∴直线l2的斜率为-$\sqrt{3}$;
∴直线方程为y-4=-$\sqrt{3}$(x-$\sqrt{3}$),
化为一般式:$\sqrt{3}$x+y-7=0.
故选:A.
点评 本题考查了直线方程的应用问题,也考查了数形结合的思想方法,是基础题.

练习册系列答案
相关题目
11.若双曲线$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{m}$=1的离心率为$\sqrt{m}$,则此双曲线的渐近线方程为( )
| A. | y=±$\frac{\sqrt{2}}{2}$x | B. | y=±$\frac{\sqrt{3}}{3}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{1}{3}$x |
18.设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x)=f(x+4),且当x∈[-2,0]时,$f(x)={(\frac{1}{2})^x}-1$,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围为( )
| A. | (1,2) | B. | (2,+∞) | C. | (1,$\root{3}{4}$) | D. | ($\root{3}{4}$,2) |
15.已知函数f(x)=$\frac{1}{2}$mcos2x+(m-2)sinx,其中1≤m≤2,若函数f(x)的最大值记为g(m),则g(m)的最小值为( )
| A. | -$\frac{1}{4}$ | B. | 1 | C. | 3-$\sqrt{3}$ | D. | $\sqrt{3}$-1 |
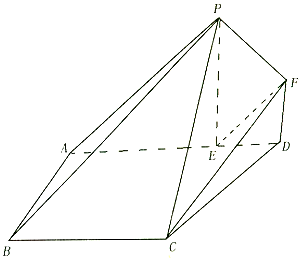 如图,在四边形ABCD中,∠BAD=90°,AD∥BC,PE⊥平面ABCD,E在AD上,FD∥PE,BC=AE=PE,DE=DF=$\frac{1}{2}$BC.
如图,在四边形ABCD中,∠BAD=90°,AD∥BC,PE⊥平面ABCD,E在AD上,FD∥PE,BC=AE=PE,DE=DF=$\frac{1}{2}$BC.